
分析 (1)根据题目中的数据可以解答本题;
(2)根据题目中的数据可以求得每次所在的位置,从而可以解答本题;
(3)根据题意可以求得行驶的总路程,从而可以解答本题.
解答 解:(1)14+(-2)+6+(-1)+10+(-3)+(-2)+12+4+(-5)+6=39,
即收工时,检修小组在A地东边,距A地39千米;
(2)刚开始为14千米,第二次是14-2=12千米,第三次是12+6=18千米,第四次为18-1=17千米,第五次为17+10=27千米,第六次为27-3=24千米,第七次为24-2=22千米,第八次为22+12=34千米,第九次为34+4=38千米,第十次为38-5=33千米,第十一次为33+6=39千米,
即距A地最远的是第十一次;
(3)0.1×(14+2+6+1+10+3+2+12+4+5+6)
=0.1×65
=6.5(升)
即若汽车每千米耗油0.1升,出发到收工时共耗油6.5升.
点评 本题考查正数和负数,解题的关键是正数和负数在题目中的实际意义.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
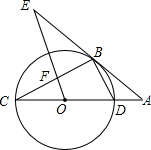 如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E.
如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
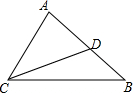 如图,下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③AC2=AD•AB;④$\frac{AC}{CD}=\frac{AB}{BC}$,其中能够判定△ABC∽△ACD的个数为( )
如图,下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③AC2=AD•AB;④$\frac{AC}{CD}=\frac{AB}{BC}$,其中能够判定△ABC∽△ACD的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
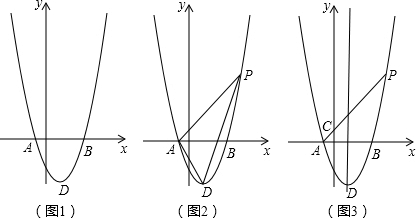
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com