
【题目】现有一面12米长的墙,某农户计划用28米长的篱笆靠墙围成一个矩形养鸡场ABCD(篱笆只围AB、BC、CD三边),其示意图如图所示.
(1)若矩形养鸡场的面积为92平方米,求所用的墙长AD.(结果精确到0.1米)(参考数据:![]() =1.41,
=1.41,![]() =1.73,
=1.73,![]() =2.24)
=2.24)
(2)求此矩形养鸡场的最大面积.

【答案】(1)所用的墙长AD约为10.5米;(2)矩形养鸡场的最大面积为96平方米
【解析】
(1)直接根据题意表示出矩形的长与宽,再表示出矩形的面积即可得出答案;
(2)利用矩形的长与宽表示出其面积,再根据二次函数的性质即可得出答案.
(1)设AD=x米,则AB=![]() (28﹣x)=(14﹣
(28﹣x)=(14﹣![]() x)米,
x)米,
根据题意,得:x(14﹣![]() x)=92,
x)=92,
解得:x1=14+2![]() ≈17.46>12,不合题意,舍去.
≈17.46>12,不合题意,舍去.
x2=14﹣2![]() =14﹣2×1.73≈10.5,
=14﹣2×1.73≈10.5,
答:所用的墙长AD约为10.5米;
(2)设矩形养鸡场ABCD的面积为S平方米,则:
S=x(14﹣![]() x)=﹣
x)=﹣![]() (x﹣14)2+98,
(x﹣14)2+98,
∵墙长12米,
∴0<x≤12.
∴当x=12时,S取最大值为:﹣![]() (12﹣14)2+98=96,
(12﹣14)2+98=96,
答:此矩形养鸡场的最大面积为96平方米.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),对称轴为x=1,与y轴的交点B在(0,2)和(0,3)之间(包含这两个点)运动.有如下四个结论:①抛物线与x轴的另一个交点是(3,0);②点C(x1,y1),D(x2,y2)在抛物线上,且满足x1<x2<1,则y1>y2;③常数项c的取值范围是2≤c≤3;④系数a的取值范围是﹣1≤a≤﹣![]() .上述结论中,所有正确结论的序号是( )
.上述结论中,所有正确结论的序号是( )
A. ①②③ B. ②③④ C. ①④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
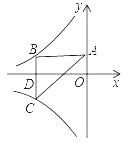
【题目】如图所示双曲线y=![]() 与y=﹣
与y=﹣![]() 分别位于第三象限和第二象限,A是y轴上任意一点,B是y=﹣
分别位于第三象限和第二象限,A是y轴上任意一点,B是y=﹣![]() 上的点,C是y=
上的点,C是y=![]() 上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=
上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y=![]() 在每个象限内,y随x的增大而减小;②若点B的横坐标为﹣3,则C点的坐标为(﹣3,
在每个象限内,y随x的增大而减小;②若点B的横坐标为﹣3,则C点的坐标为(﹣3,![]() );③k=4;④△ABC的面积为定值7,正确的有( )
);③k=4;④△ABC的面积为定值7,正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2mx+m2+1(m为常数),当自变量x的值满足﹣3≤x≤﹣1时,与其对应的函数值y的最小值为5,则m的值为( )
A. 1或﹣3 B. ﹣3或﹣5 C. 1或﹣1 D. 1或﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有2部不同的电影A、B,甲、乙、丙3人分别从中任意选择1部观看.
(1)求甲选择A部电影的概率;
(2)求甲、乙、丙3人选择同一部电影的概率(请用画树状图的方法给出分析过程,并求出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小松设计的“做圆的内接等腰直角三角形”的尺规作图过程.
已知:⊙O.

求作:⊙O的内接等腰直角三角形.
作法:如图,
①作直径AB;

②分别以点A,B为圆心,以大于![]() 的同样长为半径作弧,两弧交于M,N两点;
的同样长为半径作弧,两弧交于M,N两点;
③作直线MN交⊙O于点C,D;
④连接AC,BC.
所以△ABC就是所求作的三角形.
根据小松设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB是直径, C是⊙O上一点
∴ ∠ACB= ( ) (填写推理依据)
∵AC=BC( )(填写推理依据)
∴△ABC是等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
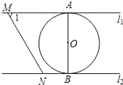
【题目】如图,直线![]() ∥
∥![]() ,⊙O与
,⊙O与![]() 和
和![]() 分别相切于点A和点B.点M和点N分别是
分别相切于点A和点B.点M和点N分别是![]() 和
和![]() 上的动点,MN沿
上的动点,MN沿![]() 和
和![]() 平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
A. ![]() B. l1和l2的距离为2
B. l1和l2的距离为2
C. 若∠MON=90°,则MN与⊙O相切 D. 若MN与⊙O相切,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为 ___________cm2 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com