练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．数据2、5、6、0、6、1、8的中位数和众数分别是（　　）
    A．0和6B．0和8C．5和6D．5和8

    分析 将题目中的数据按照从小到大排列，从而可以得到这组数据的众数和中位数，本题得以解决．

    解答 解：将2、5、6、0、6、1、8按照从小到大排列是：
    0，1，2，5，6，6，8，
    位于中间位置的数为5，
    故中位数为5，
    数据6出现了2次，最多，
    故这组数据的众数是6，中位数是5，
    故选C．

    点评 本题考查众数和中位数，解题的关键是明确众数和中位数的定义，会找一组数据的众数和中位数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．某厂按用户的月需求量x（件）完成一种产品的生产，其中x＞0，每件的售价为18万元，每件的成本y（万元）是基础价与浮动价的和，其中基础价保持不变，浮动价与月需求量x（件）成反比，经市场调研发现，月需求量x与月份n（n为整数，1≤n≤12），符合关系式x=2n2-2kn+9（k+3）（k为常数），且得到了表中的数据．
     月份n（月） 1 2
     成本y（万元/件） 11 12
     需求量x（件/月） 120 100
    （1）求y与x满足的关系式，请说明一件产品的利润能否是12万元；
    （2）求k，并推断是否存在某个月既无盈利也不亏损；
    （3）在这一年12个月中，若第m个月和第（m+1）个月的利润相差最大，求m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，四边形ABCD是正方形，△EBC是等边三角形．
    （1）求证：△ABE≌△DCE；
    （2）求∠AED的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

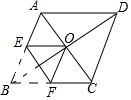    8．如图，菱形ABCD的对角线相交于点O，AC=2，BD=2$\sqrt{3}$，将菱形按如图方式折叠，使点B与点O重合，折痕为EF，则五边形AEFCD的周长为7．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

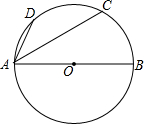    15．如图，AB为⊙O的直径，C、D为⊙O上的点，$\widehat{AD}$=$\widehat{CD}$．若∠CAB=40°，则∠CAD=25°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如果反比例函数y=$\frac{k}{x}$（k是常数，k≠0）的图象经过点（2，3），那么在这个函数图象所在的每个象限内，y的值随x的值增大而减小．（填“增大”或“减小”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

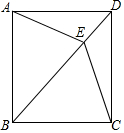    12．已知：如图，四边形ABCD中，AD∥BC，AD=CD，E是对角线BD上一点，且EA=EC．
    （1）求证：四边形ABCD是菱形；
    （2）如果BE=BC，且∠CBE：∠BCE=2：3，求证：四边形ABCD是正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

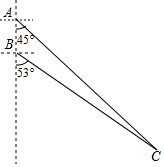    9．如图所示，我国两艘海监船A，B在南海海域巡航，某一时刻，两船同时收到指令，立即前往救援遇险抛锚的渔船C，此时，B船在A船的正南方向5海里处，A船测得渔船C在其南偏东45°方向，B船测得渔船C在其南偏东53°方向，已知A船的航速为30海里/小时，B船的航速为25海里/小时，问C船至少要等待多长时间才能得到救援？（参考数据：sin53°≈$\frac{4}{5}$，cos53°≈$\frac{3}{5}$，tan53°≈$\frac{4}{3}$，$\sqrt{2}$≈1.41）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

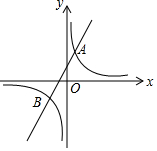    10．已知反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=ax+b的图象交于点A（1，4）和点B（m，-2）．
    （1）求这两个函数的表达式；
    （2）根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围．

    查看答案和解析>>

    同步练习册答案