
(本题满分8分)如图所示,菱形ABCD的顶点A、B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°,点A的坐标为(-2,0).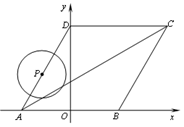
【小题1】⑴求线段AD所在直线的函数表达式.
【小题2】⑵动点P从点A出发,以每秒2个单位长度的速度,按照A→D→C→B的顺序在菱形的边上匀速运动,设运动时间为t秒.求t为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
【小题1】1)求出D(0,2)得1分 , AD解析式y=x+2…………………1分
【小题2】2)当t=2、6、10、14秒时,以点P为圆心、以1为半径的圆与对角线AC相切。
解析考点:切线的判定;待定系数法求一次函数解析式;菱形的性质。
专题:代数几何综合题。
分析:(1)在Rt△AOD中,根据OA的长以及∠BAD的正切值,即可求得OD的长,从而得到D点的坐标,然后利用待定系数法可求得直线AD的解析式。
(2)由于点P沿菱形的四边匀速运动一周,那么本题要分作四种情况考虑:
在Rt△OAD中,易求得AD的长,也就得到了菱形的边长,而菱形的对角线平分一组对角,那么∠DAC=∠BAC=∠BCA=∠DCA=30°;
①当点P在线段AD上时,若⊙P与AC相切,由于∠PAC=30°,那么AP=2R(R为⊙P的半径),由此可求得AP的长,即可得到t的值;
②③④的解题思路与①完全相同,只不过在求t值时,方法略有不同。
解答:(1)∵点A的坐标为(-2,0),∠BAD=60°,∠AOD=90°,
∴OD=OA?tan60°=2,
∴点D的坐标为(0,2),
设直线AD的函数表达式为y=kx+b,-2k+b=0;b=2,解得k=,b=2。
∴直线AD的函数表达式为y=x+2。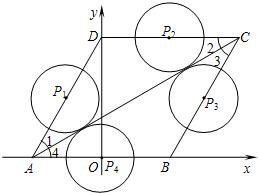
(2)∵四边形ABCD是菱形,
∴∠DCB=∠BAD=60°,
∴∠1=∠2=∠3=∠4=30°,
AD=DC=CB=BA=4,
如图所示:
①点P在AD上与AC相切时,
AP1=2r=2,
∴t1=2
②点P在DC上与AC相切时,
CP2=2r=2,
∴AD+DP2=6,
∴t2=6
③点P在BC上与AC相切时,
CP3=2r=2,
∴AD+DC+CP3=10,
∴t3=1
④点P在AB上与AC相切时,
AP4=2r=2,
∴AD+DC+CB+BP4=14,
∴t4=14,
∴当t=2、6、10、14时,以点P为圆心、以1为半径的圆与对角线AC相切。
点评:此题主要考查了一次函数解析式的确定、解直角三角形、菱形的性质、切线的判定和性质等;需要注意的是(2)题中,点P是在菱形的四条边上运动,因此要将所有的情况都考虑到,以免漏解。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
.(本题满分5分)如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.
 |
1.若将木棒沿数轴向右水平移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为20;若将木棒沿数轴向左水平移动,则当它的右端移动到A点时,则它的左端在数轴上所对应的数为5(单位:cm),由此可得到木棒长为 cm.
2.由题(1)的启发,请你借助“数轴”这个工具帮助小红解决下列问题:
问题:一天,小红去问曾当过数学老师现在退休在家的爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生;你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”,请求出爷爷现在多少岁了?
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题满分10分)如图,在平面直角坐标系中,O为原点,每个小方格的边长为1个单位长度.在第一象限内有横、纵坐标均为整数的A、B两点,且OA= OB=![]() .
.
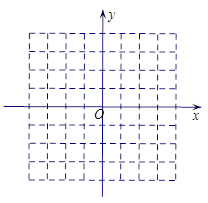
(1)写出A、B两点的坐标;
(2)画出线段AB绕点O旋转一周所形成的图形,并求其面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 交
交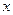 轴于
轴于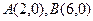 两点,交
两点,交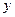 轴于点
轴于点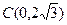 .
.
 (2)若此抛物线的对称轴与直线
(2)若此抛物线的对称轴与直线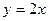 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交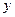 轴于点E、F两点,求劣弧EF的长;
轴于点E、F两点,求劣弧EF的长; 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com