
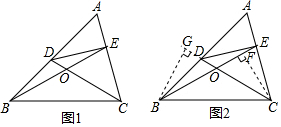
 我们知道有两条边相等的三角形叫做等腰三角形.类似的,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
我们知道有两条边相等的三角形叫做等腰三角形.类似的,我们定义:至少有一组对边相等的四边形叫做等对边四边形.分析 (1)平行四边形等;
(2)利用三角形的外角的性质,求出∠BOD即可解决问题;
(3)可证△BGO≌△CFO再证△BGD≌△CFE,可得到结论BD=CE.
解答 解:(1)平行四边形等(只要对边相等即可)
(2)∵∠A=60°,∠DCB=∠EBC=$\frac{1}{2}$∠A,
∴∠OBC=∠OCB=30°,
∴∠BOD=∠EOC=∠OBC+∠OCB=60°,
∴与∠A相等的角是∠BOD,∠EOC.
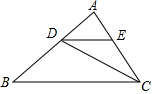
(3)结论:四边形BCED是等对边四边形.理由如下:
如图2中,作BG⊥CD于G,CF⊥BE于F.
∵∠DCB=∠EBC=$\frac{1}{2}$∠A,
∴OB=OC,
在△BGO和△CFO中,
$\left\{\begin{array}{l}{∠BGO=∠CFO}\\{∠BOG=∠COF}\\{OB=OC}\end{array}\right.$,
∴△BGO≌△CFO,
∴BG=CF,
∵∠BOD=∠A,
∴∠A+∠DOE=180°,∠ADO+∠AEO=180°,
∵∠AEO+∠CEF=180°,∠ADO=∠BDG,
∴∠BDG=∠CEF,∵∠BGD=∠CFE,
∴△BGD≌△CFE,
∴BD=CE,
∴
∴△BGD≌△CFE,
∴BD=CE.
∴四边形BCED是等对边四边形.
点评 本题考查四边形综合题、等腰三角形的判定、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 身高/cm | 146 | 151 | 153 | 154 | 156 | 157 | 158 | 159 | 160 |
| 人数 | 1 | 2 | 2 | 2 | 3 | 4 | 8 | 4 | 4 |
| 身高/cm | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 169 | |
| 人数 | 2 | 4 | 3 | 2 | 3 | 4 | 1 | 1 |
| 分组/cm | 频数累计 | 频数 | 频率 |
| 145 150 | 一 | 1 | 0.02 |
| 150 155 | 正一 | 6 | 0.12 |
| 155 160 | 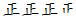 | 19 | 0.38 |
| 160 165 | 正正正 | 15 | 0.30 |
| 165 170 | 正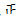 | 9 | 0.18 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.4×1011米 | B. | 140×109米 | C. | 1.4×10-11米 | D. | 1.4×10-7米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com