
| 月用水量 | 不超过12m3的部分 | 超过12m3的部分不超过18m3的部分 | 超过18m3的部分 |
| 收费标准(元/m3) | 2 | 2.5 | 3 |
分析 (1)依照题意,
当x≤12时,y=ax,
当12<x≤18时,y=6a+b(x-12),
当x>18时,y=6a+b(x-12)+c(x18),
分别把对应的x,y值代入求解可得解析式;
(2)实质是求:当x=16时,在12<x≤18内,求y值;
(3)由于45<2×12+2.5×(18-12)=54,故12<x≤18时,把y=45代入y=2.5x-6解方程即可.
解答 解:(1)依照题意,
当x≤12时,y=ax,
当12<x≤18时,y=6a+b(x-12),
当x>18时,y=6a+b(x-12)+c(x-18),
由已知得a=2,b=2.5,c=3,
当x≤12时,y=2x,
当12<x≤18时,y=12×2+2.5(x-12)=2.5x-6,
当x>18时,y=24+2.5×6+3(x-18)=3x-15;
(2)将x=16代入y=2.5x-15(12<x≤18),
得y=2.5×16-6=34(元),
答:某用户4月份用水16m3,所交水费为34元;
(3)∵45>2×12+2.5×(18-12)=39,∴12<x≤18时,把y=45代入y=3x-15得:45=3x-15,解得:x=20(m3),
答:某用户5月份交水费45元,所用水量为20m3.
点评 主要考查利用一次函数的模型解决实际问题的能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义准确的列出解析式,再把对应值代入求解.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
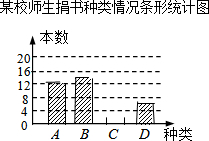 在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:| 种类 | 频数 | 百分比 |
| A.科普类 | 12 | n |
| B.文学类 | 14 | 35% |
| C.艺术类 | m | 20% |
| D.其它类 | 6 | 15% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
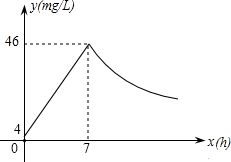 近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO,在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降,如图所示,根据题中相关信息回答下列问题:
近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO,在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降,如图所示,根据题中相关信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
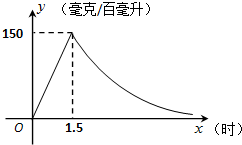 实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;1.5小时后(包括1.5小时)y与x成反比例.根据图中提供的信息,解答下列问题:
实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)成正比例;1.5小时后(包括1.5小时)y与x成反比例.根据图中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
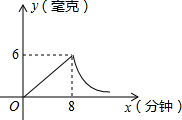 为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时室内每立方米空气中的含药量y毫克)与时间x(分钟)成正比例;药物燃烧后,y与x成反比例(如图所示).请根据图中提供的信息,解答下列问题:
为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时室内每立方米空气中的含药量y毫克)与时间x(分钟)成正比例;药物燃烧后,y与x成反比例(如图所示).请根据图中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知:如图在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,则点E的坐标为( )
已知:如图在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,则点E的坐标为( )| A. | (5,8) | B. | (5,10) | C. | (4,8) | D. | (3,10) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知关于x的二次函数y=x2+(2k-1)x+k2-1,且关于x的方程x2+(2k-1)x+k2-1=0的两根的平方和等于9.
已知关于x的二次函数y=x2+(2k-1)x+k2-1,且关于x的方程x2+(2k-1)x+k2-1=0的两根的平方和等于9.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com