
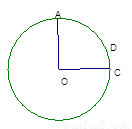
(本小题6分) 如图,OA、OC是⊙O的半径,OA=1,且OC⊥OA,点D在弧AC上,弧AD=2弧CD,在OC求一点P,使PA+PD最小,并求这个最小值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
(11·湖州)(本小题8分)
如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,OC=2。
⑴求OE和CD的长;
⑵求图中阴影部队的面积。
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(江苏扬州) 题型:解答题
(本小题8分)如图,在△ABC中, ,点D在BC上,且DC=AC,
,点D在BC上,且DC=AC,
∠ACB的平分线CF交AD于点F,点E是AB的中点,连结EF.
求证:EF∥BC;
若△ABD的面积为6,求四边形BDFE的面积.
查看答案和解析>>
科目:初中数学 来源:2011年滨海新区大港初中毕业生学业考试第一次模拟试卷数学 题型:解答题
(本小题8分)如图,四边形ABCD内接于⊙O,BD是⊙O的直径,
AE⊥CD于点E,DA平分∠BDE.
(Ⅰ)求证:AE是⊙O的切线;
(Ⅱ)若∠DBC=30°,DE="1" cm,求BD的长.
查看答案和解析>>
科目:初中数学 来源:2014届浙江省湖州市七年级上学期期中考试数学卷 题型:解答题
(本小题6分)如图,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形。

1.拼成的正方形的面积与边长分别是多少?
2.你能在3×3方格图中,连接四个格点组成面积为5的正方形吗?
3.你能把十个小正方形组成的图形纸,剪开并拼成正方形吗?若能,则它的边长是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com