
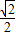 ;
; ,
, OB,
OB, x,
x, )2+(
)2+( x)2,
x)2, .
.
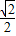 ,两圆心距=1.
,两圆心距=1.

科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源:101网校同步练习 初三数学 北师大(新课标2001/3年初审) 北师大版 题型:022
阅读下面材料:
对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A被这个圆所覆盖.
对于平面图形A,如果存在两个或两个以上的圆,使图形A上的任意一点到其中某个圆的圆心的距离都不大于这个圆的半径,则称图形A被这些圆所覆盖.
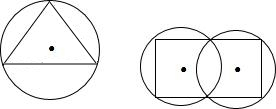
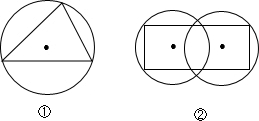
例如:图(1)中的三角形被一个圆所覆盖,图(2)中的四边形被两个圆所覆盖.
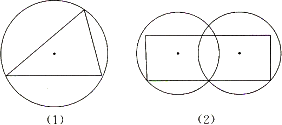
回答下列问题:
(1)边长为1 cm的正方形被一个半径为r的圆所覆盖,r的最小值是________cm;
(2)边长为1 cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是________cm;
(3)长为2 cm,宽为1 cm的矩形被两个半径为r的圆所覆盖,r的最小值是________cm,这两个圆的圆心距是________cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com