
我们知道“在三角形每一顶点处各取一个外角,它们的和就是这个三角形的外角和![]() ”.如图7-36,完成下列问题.
”.如图7-36,完成下列问题.
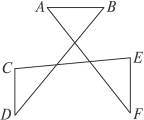
图7-36
(1)你能求出三角形的外角和等于多少吗?证明你的结论.
(2)如果将三角形三条边都向两边延长,并在每两条延长线上任取两点连结起来,那么在原三角形外又得到三个新三角形,如图所示,猜想∠A、∠B、∠C、∠D、∠E、∠F的和是多少?
(3)请用(1)的结论证明(2)的猜想.
(4)对于(2)的证明你还有其他的方法吗?请写出来与同伴交流.
答案:(1)三角形外角和等于360°.
已知:如图△ABC,∠4,∠5,∠6是外角.
求证:∠4+∠5+∠6=360°.
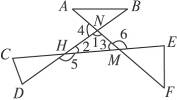
证明:∵∠4是外角,∴∠2+∠![]() 3=∠4.
3=∠4.
同理,∠1+∠3=∠5,∠2+∠1=∠6,
∴∠4+∠5+∠6=(∠2+∠3)+(∠1+∠3)+(∠2+∠1)=2(∠1+∠2+∠3).
∵∠1+∠2+∠3=180°,
∴∠4+∠5+∠6=2×180°=360°.
(2)如图,∠A+∠B+∠C+∠D+∠E+∠F=360°.
(3)∵∠4是△ABN的外角(已知),
∴∠![]() A+∠B=∠4(三角形任一外角等于与其不相邻的两内角和).
A+∠B=∠4(三角形任一外角等于与其不相邻的两内角和).
同理,∠C+∠D=∠5,∠E+∠F=∠6,
∴∠4+∠5+∠6=(∠A+∠B)+(∠C+∠D)+(∠E+∠F).
由(1)得∠4+∠5+∠6=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°(等量代换).
(4)∵∠A+∠B+∠ANB=180°,∠C+∠D+∠CHD=180°,∠E+∠F+∠EMF=180°,
∴∠A+∠B+∠ANB+∠C+∠D+∠CHD+∠E+∠F+∠EMF=180°×3=540°.
∵∠ANB=∠HNM,∠CHD=∠MHN,∠EMF=∠HMN,∠HNM+∠MHN+∠HMN=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
 .
.查看答案和解析>>
科目:初中数学 来源:学习周报 数学 沪科八年级版 2009-2010学年 第19~26期 总175~182期 沪科版 题型:044
我们知道在三角形每一个顶点处各取一个外角,它们的和就是这个三角形的外角和.
(1)如图,求出△MNP的外角和,并证明你的结论;
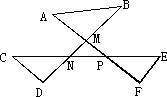
(2)猜想∠A、∠B、∠C、∠D、∠E、∠F的和是多少;
(3)请用(1)的结论证明(2)的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
我们知道“在三角形每一顶点处各取一个外角,它们的和就是这个三角形的外角和![]() ”.如图7-36,完成下列问题.
”.如图7-36,完成下列问题.

图7-36
(1)你能求出三角形的外角和等于多少吗?证明你的结论.
(2)如果将三角形三条边都向两边延长,并在每两条延长线上任取两点连结起来,那么在原三角形外又得到三个新三角形,如图所示,猜想∠A、∠B、∠C、∠D、∠E、∠F的和是多少?
(3)请用(1)的结论证明(2)的猜想.
(4)对于(2)的证明你还有其他的方法吗?请写出来与同伴交流.
查看答案和解析>>
科目:初中数学 来源:《第4章 相似三角形》2009年综合测试(B卷)(解析版) 题型:解答题
 、点P,( C)2、点O,(D)
、点P,( C)2、点O,(D) 、点O;
、点O;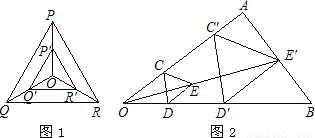
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com