
【题目】如图,已知A(-4,![]() ),B(-1,2)是一次函数y=kx+b与反比例函数y=
),B(-1,2)是一次函数y=kx+b与反比例函数y=![]() (m≠0,m<0)图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(m≠0,m<0)图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连结PC、PD,若△PCA和△PDB面积相等,求点P的坐标.
【答案】(1) -4<x<-1;(2) y=![]() x+
x+![]() ,m=-2;(3) 点P的坐标是
,m=-2;(3) 点P的坐标是![]()
【解析】试题分析:(1)观察函数图象得到当-4<x<-1时,一次函数图象都在反比例函数图象上方;
(2)先利用待定系数法求一次函数解析式,然后把B点坐标代入y=![]() 可计算出m的值;
可计算出m的值;
(3)设P点坐标为(x,![]() ,利用三角形面积公式可得到方程,解方程,再得到P的坐标.
,利用三角形面积公式可得到方程,解方程,再得到P的坐标.
试题解析:
(1)当-4<x<-1时,一次函数图象在反比例函数图象上方,故一次函数的值大于反比例函数的值.
(2)设一次函数的解析式为y=kx+b.因为y=kx+b的图象过点(-4,![]() ),(-1,2),则
),(-1,2),则
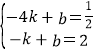
解得![]()
故一次函数的解析式为y=![]() x+
x+![]() .
.
反比例函数y=![]() 图象过点(-1,2),
图象过点(-1,2),
则m=-1×2=-2.
(3)连结PC、PD,设P(x,![]() .由△PCA和△PDB面积相等,得
.由△PCA和△PDB面积相等,得
![]()
解得x=-![]() ,则y=
,则y=![]() x+
x+![]() =
=![]() ,
,
∴点P的坐标是(-![]() ..
..


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
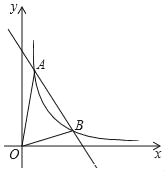
【题目】如图一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(1,6),B(n,2)两点.
(x>0)的图象交于A(1,6),B(n,2)两点.
(1)求一次函数和反比例函数的解析式
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y=![]() (k≠0)中k的值的变化情况是( )
(k≠0)中k的值的变化情况是( )
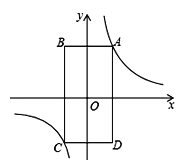
A. 一直增大 B. 一直减小 C. 先增大后减小 D. 先减小后增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某市2016年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.

(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2016年10月份的水费为620元,求该企业2016年10月份的用水量;
(3)为鼓励企业节约用水,该市自2017年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2016年收费标准收取水费外,超过80吨的部分每吨另加收![]() 元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量.
元的污水处理费,若某企业2017年3月份的水费和污水处理费共600元,求这个企业3月份的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线经过A(﹣4,0)、B(0,﹣4)、C(2,0)三点,若点M为第三象限内抛物线上一动点,△AMB的面积为S,则S的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
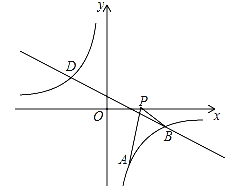
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年入夏以来,由于持续暴雨,某县遭受严重洪涝灾害,群众顿失家园。该县民政局为解决群众困难, 紧急组织了一批救灾帐篷和食品准备送到灾区。已知这批物资中,帐篷和食品共 640 件,且帐篷比食 品多 160 件。
(1)帐篷和食品各有多少件?
(2)现计划租用 A、B 两种货车共 16 辆,一次性将这批物资送到群众手中,已知 A 种货车可装帐蓬40 件和食品 10 件,B 种货车可装帐篷 20 件和食品 20 件,试通过计算帮助民政局设计几种运输 方案?
(3)在(2)条件下,A 种货 车每辆需付运费 800 元,B 种货车每辆需付运费 720 元,民政局应选择 哪种方案,才能使运输费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com