

分析 画出图形发现,符合条件的旋转角度α一共有8个,分别利用旋转角和三角形内角和及外角定理依次求出每个图形的等腰三角形.
解答 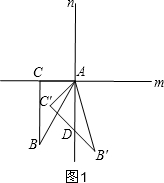 解:①当α=45°时,如图1,
解:①当α=45°时,如图1,
由旋转得:∠BAB′=45°,
∵BC∥y轴,
∴∠BAD=∠B=30°,
∴∠DAB′=45°-30°=15°,
∵∠B=∠B′=30°,
∴∠C′DA=∠DAB′+∠B′=15°+30°=45°,
∴△AC′D是等腰直角三角形;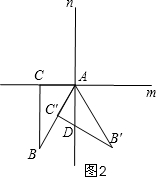
②当α=60°时,如图2,
∵BC∥y轴,
∴∠BAD=∠B=30°,
∴∠DAB′=60°-30°=30°,
∵∠B′=30°,
∴∠B′=∠DAB′,
∴△ADB′是等腰三角形;
③当α=135°时,如图3,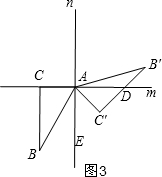
由旋转得:∠BAB′=135°,
∵∠BAE=30°,
∴∠B′AD=135°-90°-30°=15°,
∵∠B′=30°,
∴∠ADC′=30°+15°=45°,
∵∠C′=90°,
∴△AC′D是等腰直角三角形;
④当α=150°时,如图4,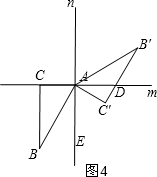
∵∠CAC′=150°,
∴∠DAC′=180°-150°=30°,
∴∠B′AD=60°-30°=30°,
∴∠B′AD=∠B′=30°,
∴△ADB′是等腰三角形;
⑤当α=225°时,如图5,
∵∠CAC′=360°-225°=135°,
∴∠DAC′=135°-90°=45°,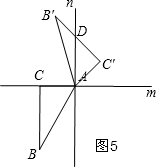
∴△AC′D是等腰直角三角形;
⑥当α=240°时,如图6,
∵∠CAC′=360°-240°=120°,
∴∠DAC′=120°-90°=30°,
∴∠B′AD=60°-30°=30°,
∴∠B′AD=∠B′=30°,
∴△ADB′是等腰三角形;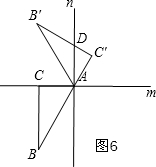 ⑦当α=315°时,如图7,
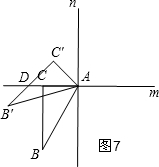
⑦当α=315°时,如图7,
∵∠CAC′=360°-315°=45°,
∴△ADC′是等腰直角三角形;
⑧当α=330°时,如图8,
∵∠CAC′=360°-330°=30°,
∴∠B′AD=60°-30°=30°,
∴∠B′AD=∠B′=30°,
∴△ADB′是等腰三角形.
综上所述,所有符合条件的旋转角度α为45°、60°、135°、150°、225°、240°、315°、330°.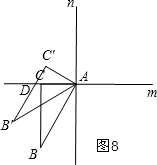
点评 本题是直角三角形的旋转变换问题,难度不大,但比较麻烦,容易丢解,要认真画图;明确对应线段的夹角就是旋转角,且旋转角都相等;本题应用了三角形的内角和及外角定理,要熟练掌握.


科目:初中数学 来源: 题型:选择题
| A. | 15° | B. | 55° | C. | 125° | D. | 165° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com