
 如图,有一块土地的形状如图所示,∠B=∠D=90°,AB=20米,BC=15米,CD=7米,计算这块土地的面积.
如图,有一块土地的形状如图所示,∠B=∠D=90°,AB=20米,BC=15米,CD=7米,计算这块土地的面积. 解:连接AC,将四边形分割成两个三角形,其面积为两个三角形的面积之和,
解:连接AC,将四边形分割成两个三角形,其面积为两个三角形的面积之和, =25(米),
=25(米),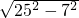 =24(米),
=24(米), AB×BC+
AB×BC+ AD×CD=234(平方米).
AD×CD=234(平方米).

科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源:2013年辽宁省盘锦市中考模拟(二)数学试卷(带解析) 题型:解答题
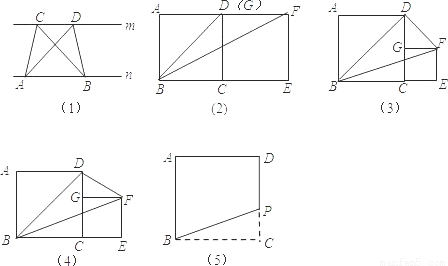
阅读理解:如图(1),已知直线m∥n,A、B 为直线n上两点,C、D为直线m上两点,容易证明:△ABC的面积=△ABD的面积.根据上述内容解决以下问题:
已知正方形ABCD的边长为4,G是边CD上一点,以CG为边作正方形GCEF.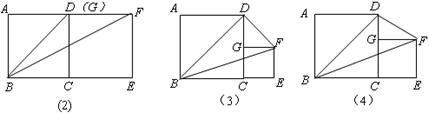
(1)如图(2),当点G与点D重合时,△BDF的面积为 ;
(2)如图(3),当点G是CD的中点时,△BDF的面积为 ;
(3)如图(4),当CG = a时,则△BDF的面积为 ,并说明理由;
探索应用:小张家有一块正方形的土地如图(5),由于修建高速公路被占去一块三角形BCP区域.现决定在DP右侧补给小张一块土地,补偿后土地变为四边形ABMD,要求补偿后的四边形ABMD的面积与原来形正方形ABCD的面积相等且M在射线BP上,请你在图中画出M点的位置,并简要叙述做法.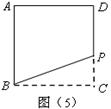
查看答案和解析>>
科目:初中数学 来源:2013年辽宁省盘锦市中考模拟(二)数学试卷(解析版) 题型:解答题
阅读理解:如图(1),已知直线m∥n,A、B 为直线n上两点,C、D为直线m上两点,容易证明:△ABC的面积=△ABD的面积.根据上述内容解决以下问题:
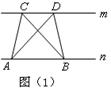
已知正方形ABCD的边长为4,G是边CD上一点,以CG为边作正方形GCEF.
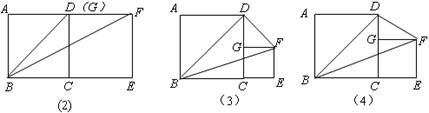
(1)如图(2),当点G与点D重合时,△BDF的面积为 ;
(2)如图(3),当点G是CD的中点时,△BDF的面积为 ;
(3)如图(4),当CG = a时,则△BDF的面积为 ,并说明理由;
探索应用:小张家有一块正方形的土地如图(5),由于修建高速公路被占去一块三角形BCP区域.现决定在DP右侧补给小张一块土地,补偿后土地变为四边形ABMD,要求补偿后的四边形ABMD的面积与原来形正方形ABCD的面积相等且M在射线BP上,请你在图中画出M点的位置,并简要叙述做法.
查看答案和解析>>
科目:初中数学 来源:2013年河北省中考数学模拟试卷(十七)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年河北省石家庄市第42中学中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com