
如图,抛物线 与x轴交于点A(—2,0),交y轴于点B(0,
与x轴交于点A(—2,0),交y轴于点B(0, ).直
).直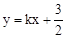 过点A与y轴交于点C,与抛物线的另一个交点是D.
过点A与y轴交于点C,与抛物线的另一个交点是D.

(1)求抛物线 与直线
与直线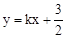 的解析式;
的解析式;
(2)设点P是直线AD下方的抛物线上一动点(不与点A、D重合),过点P作 y轴的平行线,交直线AD于点M,作DE⊥y轴于点E.探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在请求出点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,作PN⊥AD于点N,设△PMN的周长为m,点P的横坐标为x,求m与x的函数关系式,并求出m的最大值.
(1)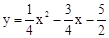 ,
, ;(2)存在,(2,-3)和(4,
;(2)存在,(2,-3)和(4,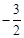 ); (3)
); (3) ,当x=3时,m的最大值是15.
,当x=3时,m的最大值是15.
【解析】
试题分析:(1)将A,B两点坐标分别代入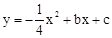 求出二次函数解析式;将A点坐标代入
求出二次函数解析式;将A点坐标代入 求出直线解析式;
求出直线解析式;
(2)首先假设出P,M点的坐标,进而得出PM的长,将两函数联立得出D点坐标,进而得出CE的长,利用平行四边形的判定得出PM=CE,得出等式方程求出即可;
(3)利用勾股定理得出DC的长,进而根据△PMN∽△CDE,得出两三角形周长之比,求出m与x的函数关系,再利用配方法求出二次函数最值即可.
试题解析:(1)∵ 经过点A(—2,0)和B(0,
经过点A(—2,0)和B(0,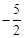 )
)
∴ ,解得
,解得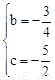 .
.
∴抛物线的解析式是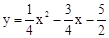 .
.
∵直线 经过点A(—2,0),∴
经过点A(—2,0),∴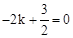 ,解得:
,解得: .
.
∴直线的解析式是 .
.
(2)存在.
设P的坐标是(x,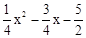 ),则M的坐标是(x,
),则M的坐标是(x,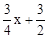 ),
),
∴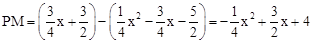 .
.
解方程 得:
得: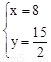 或
或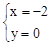 .
.
∵点D在第三象限,∴点D的坐标是(8,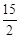 ).
).
由 令x=0得点C的坐标是(0,
令x=0得点C的坐标是(0,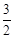 ).
).
∴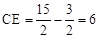 .
.
∵PM∥y轴,∴要使四边形PMEC是平行四边形,必有PM=CE,即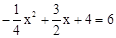 .
.
解这个方程得:x1=2,x2=4.
当x=2时,y=—3; 当x=4时,y=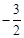 .
.
∴直线AD上方的抛物线上存在这样的点P,使四边形PMEC是平行四边形,点P的坐标是(2,-3)和(4,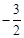 ).
).
(3)在Rt△CDE中,DE=8,CE=6 由勾股定理得:DC=10.
∴△CDE的周长是24.
∵PM∥y轴,∴∠PMN=∠DCE.
∵∠PNM=∠DEC,∴△PMN∽△CDE.
∴ ,即
,即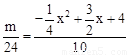 .
.
化简整理得:m与x的函数关系式是: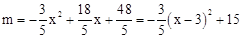 .
.
∵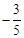 <0,∴m有最大值,当x=3时,m的最大值是15.
<0,∴m有最大值,当x=3时,m的最大值是15.
考点:1.二次函数综合题;2.单动点问题;3.曲线上点的坐标与方程的关系;4.平行四边形的判定;5.勾股定理;6.相似三角形的判定和性质;7.由实际问题列函数关系式;8.二次函数的最值.


科目:初中数学 来源: 题型:
 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.
如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是| 10 |
| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.
如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).
如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com