
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
分析 先根据题意得出a,b的值,再判断出函数的增减性,根据a,b的大小即可得出结论.
解答 解:∵关于的方程x2+2(1+a)x+(3a2+4ab+4b2+2)=0有实数根,
∴△≥0,即[2(1+a)]2-4(3a2+4ab+4b2+2)≥0,
∴(a+2b)2+(a-1)2≤0 ①
∵(a+2b)2≥0且(a-1)2≥0,得(a+2b)2+(a-1)2≥0 ②
∴只有当(a+2b)2=0且(a-1)2=0不等式①和②才能同时成立.
∴a=1,b=-$\frac{1}{2}$.
∵一次函数y=kx中k>0,
∴y随x的增大而增大,
∵1>-$\frac{1}{2}$,
∴y1>y2,
∴y1-y2>0.
故选A.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
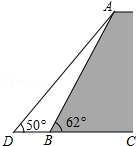 如图,一堤坝的坡角∠ABC=62°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到1米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
如图,一堤坝的坡角∠ABC=62°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到1米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 垂直于弦的直径平分弦 | |
| B. | 若a>b,c>0,则ac>bc | |
| C. | 反比例函数y=$\frac{k}{x}$,当k>0时,y随x的增大而减少 | |
| D. | 对角线互相平分且垂直的四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com