
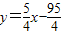 与x轴和y轴的交点分别为A、B,则线段AB上(包括端点A、B)横坐标和纵坐标都是整数的点有 个.
与x轴和y轴的交点分别为A、B,则线段AB上(包括端点A、B)横坐标和纵坐标都是整数的点有 个.  ;令y=0,则x=19,
;令y=0,则x=19,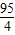 )、(19,0)
)、(19,0)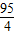 ,不符合题意;
,不符合题意;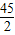 ,不符合题意;
,不符合题意;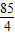 ,不符合题意;
,不符合题意;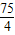 ,不符合题意
,不符合题意 ,不符合题意
,不符合题意 ,不符合题意;
,不符合题意;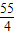 ,不符合题意;
,不符合题意;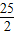 ,不符合题意;
,不符合题意;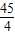 ,不符合题意;
,不符合题意;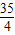 ,不符合题意;
,不符合题意;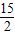 ,不符合题意;
,不符合题意; ,不符合题意;
,不符合题意;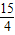 ,不符合题意;
,不符合题意; ,不符合题意;
,不符合题意; ,不符合题意;
,不符合题意;

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (1997•上海)已知直角坐标系内有一条直线和一条曲线,这条直线和x轴、y轴分别交于点A和点B,且OA=OB=1,这条曲线是函数y=
(1997•上海)已知直角坐标系内有一条直线和一条曲线,这条直线和x轴、y轴分别交于点A和点B,且OA=OB=1,这条曲线是函数y=| 1 | 2x |
查看答案和解析>>
科目:初中数学 来源: 题型:
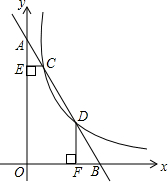 如图,在平面直角坐标系中,直线AB与y轴和x轴分别交于点A、点B,与反比例函数y=
如图,在平面直角坐标系中,直线AB与y轴和x轴分别交于点A、点B,与反比例函数y=| m | x |
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(福建三明卷)数学(带解析) 题型:解答题
已知直线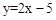 与x轴和y轴分别交于点A和点B,抛物线
与x轴和y轴分别交于点A和点B,抛物线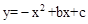 的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.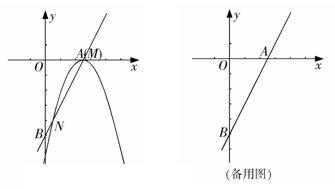
(1)如图,当点M与点A重合时,求:
①抛物线的解析式;(4分)
②点N的坐标和线段MN的长;(4分)
(2)抛物线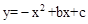 在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.(4分)
在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.(4分)
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(福建三明卷)数学(解析版) 题型:解答题
已知直线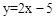 与x轴和y轴分别交于点A和点B,抛物线
与x轴和y轴分别交于点A和点B,抛物线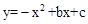 的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.

(1)如图,当点M与点A重合时,求:
①抛物线的解析式;(4分)
②点N的坐标和线段MN的长;(4分)
(2)抛物线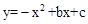 在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.(4分)
在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.(4分)
查看答案和解析>>
科目:初中数学 来源:期中题 题型:解答题
 与x轴和y轴交于点A、C两点,抛物线
与x轴和y轴交于点A、C两点,抛物线 经过点A、C,点B是抛物线与x轴的另一个交点.
经过点A、C,点B是抛物线与x轴的另一个交点.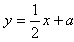 与(1)中所求的抛物线交于M、N两点,问:是否存在a的值,使得∠MON=90°,若存在,求出a的值,若不存在,请说明理由。
与(1)中所求的抛物线交于M、N两点,问:是否存在a的值,使得∠MON=90°,若存在,求出a的值,若不存在,请说明理由。 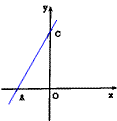
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com