
科目:初中数学 来源:同步轻松练习 八年级 数学 上 题型:044
某巡逻船在码头外巡逻,离开码头的距离s(米)与巡逻时间t(分)的函数关系可用下图中的曲线表示.同时一艘游船到码头的距离s(米)与时间t(分)的函数关系式为s=50t+500.
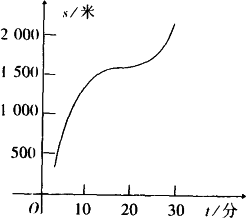
(1)在同一直角坐标系中画出函数s=50t+500的图象.
(2)根据图象估计在哪些时刻游船和巡逻船到码头的距离相同(时间精确到分,允许误差±1分).
查看答案和解析>>
科目:初中数学 来源:伴你学·数学·九年级·下册 题型:022
在同一直角坐标系中作出函数y=3x2,y=3(x-1)2和y=3(x+2)2的图象,然后根据图象填空:

抛物线y=3x2的顶点坐标是( ),对称轴是________,开口向________;
抛物线y=3(x-1)2的顶点坐标是( ),对称轴是________,开口向________;
抛物线x=3(x+2)2的顶点坐标是( ),对称轴是________,开口向________.
可以发现,抛物线y=3(x-1)2,y=3(x+2)2与抛物线y=3x2的形状、开口大小相同,只是抛物线的位置和对称轴发生了变化.把抛物线y=3x2沿x轴向________平移________个单位即可得到抛物线y=3(x-1)2;把抛物线y=3x2沿x轴向________平移________个单位即可得到抛物线y=3(x+2)2.
查看答案和解析>>
科目:初中数学 来源:伴你学·数学·九年级·下册 题型:022
在同一直角坐标系中作出函数y=x2,y=(x-2)2和y=(x-2)2+3的图象,然后根据图象填空:

抛物线y=x2的顶点坐标是( ),对称轴是________,开口向________;
抛物线y=(x-2)2的顶点坐标是( ),对称轴是________,开口向________;
抛物线y=(x-2)2+3的顶点坐标是( ),对称轴是________,开口向________.
可以发现,抛物线y=(x-2)2,y=(x-2)2+3与抛物线y=x2的形状、开口大小相同,只是抛物线的位置发生了变化.把抛物线y=x2沿x轴向________平移________个单位即可得到抛物线y=(x-2)2;把抛物线y=(x-2)2沿y轴向________平移________个单位即可得到抛物线y=(x-2)2+3;也就是说,把抛物线y=x2沿x轴向________平移________个单位,再沿y轴向________平移________个单位即可得到抛物线y=(x-2)2+3.
还可以发现,对于y=x2,当x<0时y的值随x值的增大而________,当x>0时y的值随x值的增大而________;对于y=k(x-2)2,当x<2时,y的值随x值的增大而________,当x>2时,y的值随x值的增大而________;对于y=(x-2)2+3,当x<2时,y的值随x值的增大而________,当x>2时,y的值随x值的增大而________.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com