
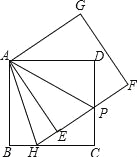
【题目】如图,在边长为6的正方形ABCD中,将正方形ABCD绕点A逆时针旋转角度α(0°<α<90°),得到正方形AEFG,EF交线段CD于点P,FE的延长线交线段BC于点H,连接AH、AP.
(1)求证:△ADP≌△AEP;
(2)①求∠HAP的度数;②判断线段HP、BH、DP的数量关系,并说明理由;
(3)连接DE、EC、CF、DF得到四边形CFDE,在旋转过程中,四边形CFDE能否为矩形?若能,求出BH的值;若不能,请说明理由.
【答案】(1)证明详见解析;(2)①45°;②HP=HE+EP=HB+DP;(3)能,2.
【解析】
试题分析:(1)根据旋转变换的性质得到AB=AE,∠AEP=∠ABH=90°,根据正方形的性质得到AD=AB,∠D=90°,根据直角三角形的全等的判定定理证明即可;
(2)证明Rt△COH≌Rt△CDH,得到∠OCH=∠DCH,HO=DH,等量代换即可;
(3)根据矩形的判定定理证明四边形AEBD是矩形,设点H的坐标为(x,0),根据勾股定理列出方程,解方程求出x的值,得到点H的坐标.
试题解析:(1)∵将正方形ABCD绕点A逆时针旋转角度α,
∴AB=AE,∠AEP=∠ABH=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠D=90°,
∴AE=AD,∠D=∠AEP=90°
在Rt△ADP与Rt△AEP中,
AD=AE,AP=AP,
∴Rt△ADP≌Rt△AEP;
(2)∵∠AEP=90°,
∴∠AEH=90°,
在Rt△ABH与Rt△AEH中,
AB=AE,AH=AH,
∴Rt△ABH≌Rt△AEH,
∴∠BAH=∠EAH,BO=HE,
∵Rt△AEP≌Rt△ADP,
∴∠EAP=∠DAP,EP=DP,
∴∠HAP=∠HAE+∠EAP=![]() ∠BAD=45°,
∠BAD=45°,
HP=HE+EP=HB+DP;
(3)当P是CD中点时,四边形CFDE是矩形,
∵P是CD中点,
∴DP=CP=![]() CD,
CD,
由(2)得EP=DP,
又∵CD=EF,
∴DG=![]() DE,
DE,
∴DP=PC=PE=PF,
∴四边形CFDE是矩形,
设BH=x,
则HE=BH=x,PE=PD=PC=3,CH=6﹣x,
由勾股定理得,![]() ,
,
解得,x=2,即BH=2.



 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
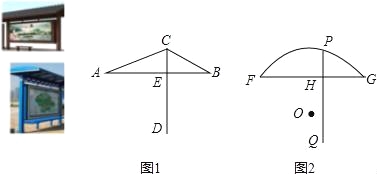
【题目】我市城市风貌提升工程正在火热进行中,检查中发现一些破旧的公交车候车亭有碍观瞻,现准备制作一批新的公交车候车亭,查看了网上的一些候车亭图片后,设计师画了两幅侧面示意图,AB,FG均为水平线段,CD⊥AB,PQ⊥FG,E,H为垂足,且AE=FH,AB=FG=2米,图1中tanA=![]() ,tanB=
,tanB=![]() ,图2点P在弧FG上.且弧FG所在圆的圆心O到FG,PQ的距离之比为5:2,
,图2点P在弧FG上.且弧FG所在圆的圆心O到FG,PQ的距离之比为5:2,
(1)求图1中的CE长;
(2)求图2中的PH长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=A1B,A1C=A1A2,A2D=A2A3,A3E=A3A4,∠B=20°,则∠A4=( )

A. 10° B. 15° C. 30° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,∠B=∠C=90 ,M是BC的中点,DM平分∠ADC.
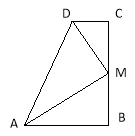
(1)若连接AM,则AM是否平分∠BAD?请你证明你的结论;
(2)线段DM与AM有怎样的位置关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列算式:(1)3a+2b=5ab;(2)5y2﹣2y2=3;(3)7a+a=7a2;(4)4x2y﹣2xy2=2xy中正确的有( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABO中,A,B两点的坐标分别为(2,4),(7,2),C,G,F,E分别为过A,B两点所作的y轴、x轴的垂线与y轴、x轴的交点.求△AOB的面积.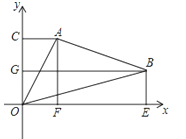
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com