
已知二次函数y=ax2+bx的图象经过点A(-5,0)和点B,其中点B在第一象限,且OA=OB,tan∠BAO=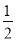
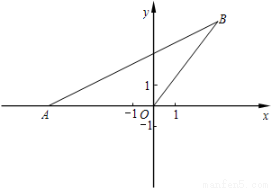
(1)求点B的坐标。
(2)求二次函数的解析式。
(3)过点B作直线BC平行于x轴,直线BC与二次函数图象的另一个交点为C,连结AC,如果点P在x轴上,且△ABC和△PAB相似,求点P的坐标。
(1)点B的坐标是(3,4),(2)y=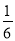 x2+
x2+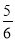 x;(3)点P的坐标为(6,0)或(
x;(3)点P的坐标为(6,0)或(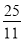 ,0).
,0).
【解析】
试题分析:(1)过点B作BD⊥x轴,垂足为点D,根据余切的定义可设BD=x,AD=2x,在Rt△ODB中根据勾股定理可计算出x,则BD=4,OD=3,所以点B的坐标是(3,4);
(2)利用待定系数法可确定二次函数的解析式;
(3)先确定C点的坐标为(-8,4),则BC=11,AB=4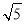 ,由CB∥x轴得到∠ABC=∠BAP,再分类讨论:当△ABC∽△BAP;当△ABC∽△PAB,然后利用比例线段求AP的长,从而确定P点坐标.
,由CB∥x轴得到∠ABC=∠BAP,再分类讨论:当△ABC∽△BAP;当△ABC∽△PAB,然后利用比例线段求AP的长,从而确定P点坐标.
试题解析:(1)过点B作BD⊥x轴,垂足为点D,如图,
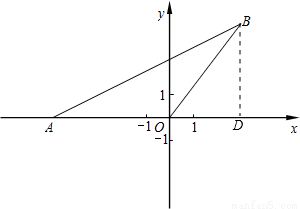
在Rt△ADB中,∠ADB=90°,tan∠BAO=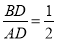
设BD=x,AD=2x,
∵OA=0B=5,
∴OD=2x-5,
在Rt△ODB中,∵OD2+BD2=OB2,
∴(2x-5)2+x2=52,
解得x1=4,x2=0(不合题意,舍去),
∴BD=4,OD=3,
∴点B的坐标是(3,4),
(2)根据题意得
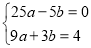 ,
,
解这个方程组,得
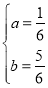 ,
,
∴二次函数的解析式是y=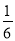 x2+
x2+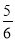 x;
x;
(3)∵直线BC平行于x轴,
∴C点的纵坐标为4,
设C点的坐标为(m,4).
由题意得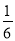 m2+
m2+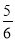 m=4,
m=4,
解得m1=3(不合题意,舍去),m2=-8,
∴C点的坐标为(-8,4),BC=11,AB=4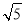
∵∠ABC=∠BAP,
①如果△ABC∽△BAP,那么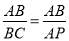
∴AP=11,点P的坐标为(6,0),
②如果△ABC∽△PAB,那么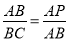 ,
,
∴AP=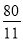 ,点P的坐标为(
,点P的坐标为(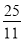 ,0),
,0),
综上所述,点P的坐标为(6,0)或(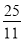 ,0).
,0).
考点:待定系数法求二次函数解析式.


科目:初中数学 来源:2014-2015学年黑龙江省哈尔滨市道里区九年级上学期期末调研测试数学试卷(解析版) 题型:填空题
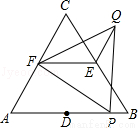
如图,△ABC和△FPQ均是等边三角形,点D、E、F分别是△ABC三边的中点,点P在AB边上,连接EF、QE.若AB=6,PB=1,则QE= 2 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市阜宁县八年级上学期期中调研数学试卷(解析版) 题型:填空题
已知一直角三角形的木板,三边的平方和为800 cm2,则斜边长为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市阜宁县八年级上学期期中调研数学试卷(解析版) 题型:选择题
下列结论正确的是
A.有两个锐角相等的两个直角三角形全等
B.一条斜边对应相等的两个直角三角形全等
C.两个等边三角形全等
D.顶角和底边对应相等的两个等腰三角形全等
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省金华市青春共同体九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,AB是⊙O的直径,C是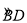 的中点,CE⊥AB于 E,BD交CE于点F.
的中点,CE⊥AB于 E,BD交CE于点F.
(1)求证:CF﹦BF;
(2)若CD=6,AC=8,求⊙O的半径及CE的长。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省金华市青春共同体九年级上学期期中考试数学试卷(解析版) 题型:填空题
△ABC中,∠A、∠B都是锐角,若sinA=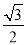 ,cosB=
,cosB=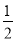 ,则∠C= .
,则∠C= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省潍坊地区九年级上学期期末质量评估数学试卷(解析版) 题型:解答题
(本题满分10分)市某楼盘准备以每平方米6 000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4 860元的均价开盘销售.
(1)求平均每次下调的百分率.
(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com