
【题目】如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC,连接OD,OA.
(1)求∠ODC的度数;
(2)若OB=2,OC=3,求AO的长.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】(阅读理解)小海喜欢研究数学问题,在计算整式加减(﹣4x2﹣7+5x)+(2x+3x2)的时候,想到了小学的列竖式加减法,令A=﹣4x2﹣7+5x,B=2x+3x2,然后将两个整式关于x进行降幂排列,A=﹣4x2+5x﹣7,B=3x2+2x,最后只要写出其各项系数对齐同类项进行竖式计算如下:
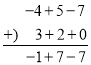
所以,(﹣4x2﹣7+5x)+(2x+3x2)=﹣x2+7x﹣7.
(模仿解题)若A=﹣4x2y2+2x3y﹣5xy3+2x4,B=3x3y+2x2y2﹣y4﹣4xy3,请你按照小海的方法,先对整式A,B关于某个字母进行降幂排列,再写出其各项系数进行竖式计算A﹣B,并写出A﹣B的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家水果店以每千克2元的价格购进某种水果若干千克,然后以每千克4元的价格出售,每天可售出100千克,通过调查发现,这种水果每千克的售价每降低1元,每天可多售出200千克.
(1)若将这种水果每千克的售价降低![]() 元,则每天销售量是多少千克?(结果用含
元,则每天销售量是多少千克?(结果用含![]() 的代数式表示)
的代数式表示)
(2)若想每天盈利300元,且保证每天至少售出260千克,那么水果店需将每千克的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.
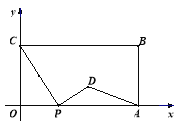
(1)请用含t的代数式表示出点D的坐标;
(2)求t为何值时,△DPA的面积最大,最大为多少?
(3)在点P从O向A运动的过程中,△DPA能否成为直角三角形?若能,求t的值.
若不能,请说明理由;
(4)请直接写出随着点P的运动,点D运动路线的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,点
中,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() .连接
.连接![]() ,过点
,过点![]() 作
作![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() .
.
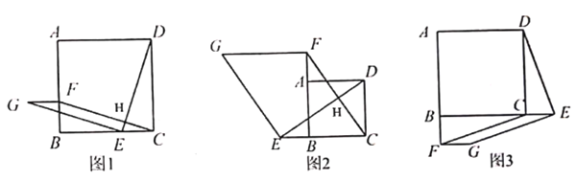
(1)请判断:![]() 与
与![]() 的数量关系是________________,位置关系是___________________;
的数量关系是________________,位置关系是___________________;
(2)如图2,若点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,A, B是直线l上的两点,点B关于AD的对称点为M,连接![]() 交AD于F点.
交AD于F点.
(1)若![]() ,如图,
,如图,
①依题意补全图形;
②判断MF与FC的数量关系是 ;

(2)如图,当![]() 时,
时,![]() ,CD的延长线相交于点E,取
,CD的延长线相交于点E,取![]() E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.
E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.

(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com