
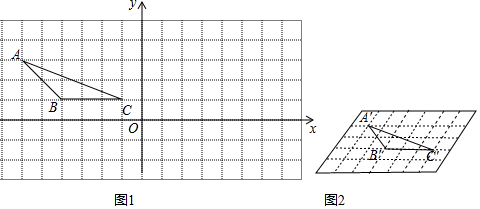
���� ��1����ֱ�ӵõ��ԳƵ�����꼴�ɣ�
�ڻ�ͼ��
�۸������еĶ��壺���ڶԱ߱��ڱߣ���tan��A2B2C2=$\frac{2}{5}$��
��2��������A'E������ֱ�������Σ����ù��ɶ�����A'E��EC'�ij����ɵý��ۣ�
��� 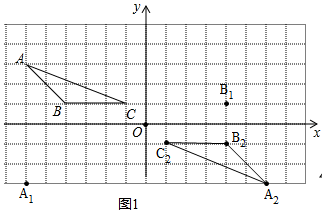 �⣺��1���ٵ�A����x��ĶԳƵ�A1�������ǣ�-6��-3������B����y��ĶԳƵ�B1�������ǣ�4��1����
�⣺��1���ٵ�A����x��ĶԳƵ�A1�������ǣ�-6��-3������B����y��ĶԳƵ�B1�������ǣ�4��1����
�ʴ�Ϊ����-6��-3������4��1����
����ͼ1��ʾ��
��tan��A2B2C2=$\frac{2}{5}$��
�ʴ�Ϊ��$\frac{2}{5}$��
��2����ͼ2����A'��A'E��B��C����E���ӳ�C��B����D��ʹDC'=5������A'D��
Rt��A��ED�У��ߡ�A��DE=60�㣬A'D=2��
��DE=1��A'E=$\sqrt{3}$��
��EC'=5-1=4��
Rt��A��EC����tan��A'C'B'=$\frac{A��E}{EC��}$=$\frac{\sqrt{3}}{4}$��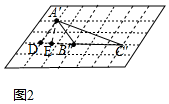
�ʴ�Ϊ��$\frac{\sqrt{3}}{4}$��
���� ���⿼���˹���ԭ�㡢x�ᡢy��Գƣ����ε����ʣ���ֱ�������Σ������������еĶ����ǹؼ���


 �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
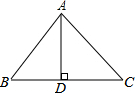 ��ͼ���ڡ�ABC�У�AD��BC������ΪD����B=60�㣬��C=45�㣬AC=3$\sqrt{2}$��
��ͼ���ڡ�ABC�У�AD��BC������ΪD����B=60�㣬��C=45�㣬AC=3$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2a}$ | B�� | $\sqrt{9a}$ | C�� | a$\sqrt{2}$ | D�� | $\sqrt{4{a}^{2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
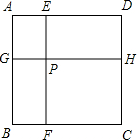 ��ͼ���߳�Ϊa��������ABCD���������ƽ�е��߶�EF��GH�ָ���ĸ�С���Σ�EF��GH���ڵ�P������AF��AH��
��ͼ���߳�Ϊa��������ABCD���������ƽ�е��߶�EF��GH�ָ���ĸ�С���Σ�EF��GH���ڵ�P������AF��AH���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com