
如图,△ABC中,AB=AC,D、E、F分别在BC、AB、AC上,且BE=CD,BD=CF.
(1)求证:DE=DF;
(2)当∠A的度数为多少时,△DEF是等边三角形,并说明理由.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
直角三角形纸片的两直角边长分别为6,8,现将△ABC如图4那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是 ( )
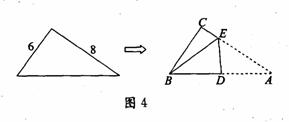 A.
A. 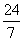
B. 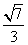
C. 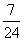
D. 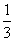
查看答案和解析>>
科目:初中数学 来源: 题型:
.如图,两直线AB,CD相 交于点O,已知OE平分∠BOD,且∠AOC:∠AOD=3:7,
交于点O,已知OE平分∠BOD,且∠AOC:∠AOD=3:7,
(1)求∠DOE的度数;(5分)
(2)若∠E0F是直角,求∠AOF的度数。(3分)
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
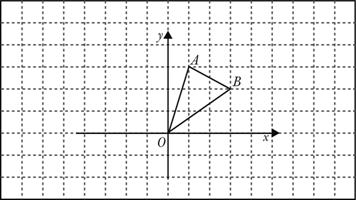
如图所示,在边长为1个单位的小正方形网格中,△AOB的顶点均在格点上,A(1,3),B(3,2).
(1)B点关于y对称的点的坐标为 ;
(2)将△AOB向左平移3个单位长度得到△ ,请画出△
,请画出△ ;
;
(3)在(2)的条件下, 点的坐标为 .
点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
题目“某幼儿园给小朋友分苹果,若每人分3个则剩1个;若每人分4个则差2个。求苹果有多少个?”,解答时设共 有x个苹果分给小朋友,列出的方程可以是( )
有x个苹果分给小朋友,列出的方程可以是( )
A. 3x+4=4x-2 B. =
= C.
C.  =
= D.
D.  =
=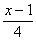
查看答案和解析>>
科目:初中数学 来源: 题型:
某次足球邀请赛的记分规则及奖励方案如 下表:
下表:
| 胜一场 | 平一场 | 负一场 | |
| 积分 | 3 | 1 | 0 |
| 奖励(元/每人) | 1500 | 700 | 0 |
已知12轮(即每队比赛12场)过后,A队积分达到19分。
(1)试判断A队胜、平、负各几场?
(2)若每一场每名参赛队员均得出场费500元,设A队中一位参赛队员所得的奖金与出场费的和为W(元),试求W的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com