
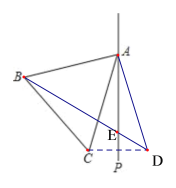
【题目】如图,在等边三角形ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形;
(2)若∠PAC=20°,求∠AEB的度数;

【答案】(1)见详解;(2)60°
【解析】
(1)作出点C关于直线AP的对称点为点D,连接AD,BD,即可得到所作图形;
(2)由等边三角形的性质和轴对称的性质,可得AB=AD,∠BAD=100°,结合三角形内角和定理,求出∠ADB的度数,然后由三角形外角的性质,即可求解.
(1)补全图形,如图所示:
(2)∵点C关于直线AP的对称点为点D,
∴AC=AD,∠PAD=∠PAC=20°,
∵三角形ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴AB=AD,∠BAD=60°+20°+20°=100°,
∴∠ADB=(180°-100°)÷2=40°,
∴∠AEB=∠ADB+∠PAD=40°+20°=60°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨,则每吨按政府补贴优惠价a元收费;若每月用水量超过14吨,则超过部分每吨按市场调节价b元收费.小刘家3月份用水10吨,交水费20元;4月份用水16吨,交水费35元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小刘预计他家5月份用水不会超过22吨,那么小刘家5月份最多交多少元水费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE;
(2)如果AB=12,BC=15,求tan∠FBE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A5B5A6的边长为( )

A.6B.16C.32D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣(2k+1)x+k2+k(k>0)
(1)当k=![]() 时,将这个二次函数的解析式写成顶点式;
时,将这个二次函数的解析式写成顶点式;
(2)求证:关于x的一元二次方程x2﹣(2k+1)x+k2+k=0有两个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三张形状、大小相同但画面不同的风景图片,都按同样的方式剪成相同的三段,然后将上、中、下三段分别混合洗匀,从三堆图片中随机各抽出一张, 求这三张图片恰好组成一张完整风景图片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 交
交![]() 轴于点
轴于点![]() 、点
、点![]() ,交
,交![]() 轴于点C,且S△ABC=6.
轴于点C,且S△ABC=6.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求△ABC的外接圆与抛物线的对称轴的交点坐标;
(3)点E为抛物线上的一动点(点![]() 异于
异于![]() ,且
,且![]() 在对称轴右侧),直线
在对称轴右侧),直线![]() 交对称轴于N,
交对称轴于N,
直线BE交对称轴于![]() ,对称轴交
,对称轴交![]() 轴于
轴于![]() ,试确定
,试确定![]() 、
、![]() 的数量关系并说明理由.
的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,E是OB的中点,过点B作BF∥AC交AE的延长线于点F,连接CF.

(1)求证:△AOE≌△FBE;
(2)求证:四边形BOCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BC=20 cm,P,Q,M,N分别从A,B,C,D出发,沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=x cm(x≠0),则AP=2x cm,CM=3x cm,DN=x2 cm,
(1)当x为何值时,点P,N重合;
(2)当x为何值是,以P,Q,M,N为顶点的四边形是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com