
分析 (1)将原式根据多项式乘以多项式法则展开后合并同类项,由积中不含x项与x3项可知x项与x3项的系数均等于0,可得关于p、q的方程组,解方程组即可;
(2)由(1)中p、q的值得pq=-1,将原式整理变形成4p2(pq)2+$\frac{1}{3pq}$+(pq)2013•q,再将p、q、pq的值代入计算即可.
解答 解:(1)(x2+px-$\frac{1}{3}$)(x2-3x+q)=x4-3x3+qx2+px3-3px2+pqx-$\frac{1}{3}$x2+x-$\frac{1}{3}$q
=x4+(p-3)x3+(q-3p-$\frac{1}{3}$)x2+(pq+1)x-$\frac{1}{3}$q,
∵积中不含x项与x3项,
∴$\left\{\begin{array}{l}{p-3=0}\\{pq+1=0}\end{array}\right.$,
解得:p=3,q=-$\frac{1}{3}$;
(2)∵p=3,q=-$\frac{1}{3}$,
∴pq=-1,
∴(-2p2q)2+(3pq)-1+p2013q2014=4p4q2+$\frac{1}{3pq}$+p2013q2014
=4p2(pq)2+$\frac{1}{3pq}$+(pq)2013•q
=4×32×1-$\frac{1}{3}$+$\frac{1}{3}$
=36.
点评 本题主要考查多项式乘以多项式的法则.注意不要漏项、漏字母、有同类项的合并同类项,解题的关键是正确求出p,q的值.


科目:初中数学 来源: 题型:解答题
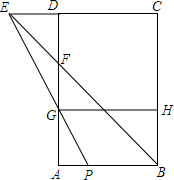 如图,矩形ABCD中,点F在AD上,AF=AB=12,点G是AF的中点,延长CD和BF交于点E,EG的延长线交AB于点P,GH∥AB交BC于点H,已知AP比ED小1.
如图,矩形ABCD中,点F在AD上,AF=AB=12,点G是AF的中点,延长CD和BF交于点E,EG的延长线交AB于点P,GH∥AB交BC于点H,已知AP比ED小1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
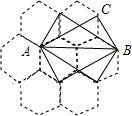 蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的蜂型网络,正六边形的顶点称为格点,如果一个三角形的三个顶点都在格点上,称之为格点三角形.如图以AB为斜边的格点直角三角形共有4个,△ABC是其中之一,则在蜂巢型网络中,与△ABC全等的格点三角形(包括△ABC)共有84.
蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的蜂型网络,正六边形的顶点称为格点,如果一个三角形的三个顶点都在格点上,称之为格点三角形.如图以AB为斜边的格点直角三角形共有4个,△ABC是其中之一,则在蜂巢型网络中,与△ABC全等的格点三角形(包括△ABC)共有84.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点M为正方形ABCD的边AB(或BA)延长线上任意一点,MN⊥DM且与∠ABC外角的平分线交于点N,此时MD与MN有何数量关系?并加以证明.
如图,点M为正方形ABCD的边AB(或BA)延长线上任意一点,MN⊥DM且与∠ABC外角的平分线交于点N,此时MD与MN有何数量关系?并加以证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com