
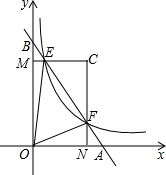
 如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于A,B与反比例函数y=$\frac{k}{x}$(k>0且为常数)在第一象限的图象交于点E,F,过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C,若$\frac{BE}{BF}$=$\frac{2}{5}$,则$\frac{{S}_{△CEF}}{{S}_{△OEF}}$=$\frac{3}{7}$.
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于A,B与反比例函数y=$\frac{k}{x}$(k>0且为常数)在第一象限的图象交于点E,F,过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C,若$\frac{BE}{BF}$=$\frac{2}{5}$,则$\frac{{S}_{△CEF}}{{S}_{△OEF}}$=$\frac{3}{7}$. 分析 根据E,F都在反比例函数的图象上得出假设出E,F的坐标,进而分别得出△CEF的面积S1以及△OEF的面积S2,然后即可得出答案.
解答 解:设△CEF的面积为S1,△OEF的面积为S2,过点F作FD⊥BO于点D,EW⊥AO于点W,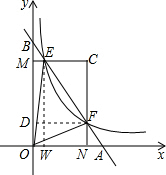
∵$\frac{BE}{BF}$=$\frac{2}{5}$,
∴$\frac{ME}{DF}$=$\frac{2}{5}$,
∵ME•EW=FN•DF,
∴$\frac{ME}{DF}$=$\frac{FN}{EW}$=$\frac{2}{5}$,
设E点坐标为:(2x,5y),则F点坐标为:(5x,2y),
∴△CEF的面积为:S1=$\frac{1}{2}$(5x-2x)(5y-2y)=$\frac{1}{2}$(5-2)2xy=$\frac{9}{2}$xy,
∵△OEF的面积为:S2=S矩形CNOM-S1-S△MEO-S△FON
=MC•CN-$\frac{1}{2}$(5-2)2xy-$\frac{1}{2}$ME•MO-$\frac{1}{2}$FN•NO
=5x•5y-$\frac{1}{2}$(5-2)2xy-$\frac{1}{2}$•2x•5y-$\frac{1}{2}$•2y•5x=$\frac{21}{2}$xy
∴$\frac{{S}_{△CEF}}{{S}_{△OEF}}$=$\frac{3}{7}$.
故答案为:$\frac{3}{7}$.
点评 此题主要考查了反比例函数的综合应用以及三角形面积求法,根据已知表示出E,F的点坐标是解题关键,难度较大,要求同学们能将所学的知识融会贯通.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(cm) | 185 | 180 | 185 | 180 |
| 方差 | 3.6 | 3.6 | 7.4 | 8.1 |
| A. | 丁 | B. | 丙 | C. | 乙 | D. | 甲 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
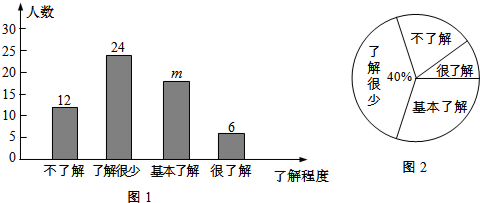
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{9}{4}$ | C. | 3 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
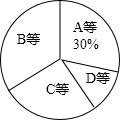 某校为了解七年级男生1000米跑步的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四等,并绘制成频数分布表和扇形统计图.
某校为了解七年级男生1000米跑步的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四等,并绘制成频数分布表和扇形统计图.| 等级 | 成绩(得分) | 频数(人数) | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | m | |
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | y | n | |
| D | 5分以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com