
���Ķ����в��ϣ��ٽ���������⣮
���ϣ�����ѧ��һ�ź����ء�����Ȥ��ѧ�ʣ�������ѧ�У�ֱ�ӿ��Կ�������Ϣ��Ϊ���룬���ܺ����Ϣ��Ϊ���룬�κ�����ֻҪ�ҵ�������������Ķ�Ӧ��ϵ�D�D��Կ���Ϳ�����������
����ѧ����ѧ���й�ϵ�ģ�Ϊ�ˣ�����һ����ѧ��ȤС�龭���о�ʵ�飬����ѧ��һ�κ���֪ʶ������һ����Կ�ı��Ƴ����������������һ������ĸ�D�D������ձ�����
| ��ĸ | A | B | C | D | E | F | G | H | I | J | K | L | M |
| ���� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| ��ĸ | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| ���� | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
���磬��y=3x+13Ϊ��Կ���������š����ֽ��м���ת����õ��±���
| �� �� | �� | �� | |||
| ƴ �� | Z | I | X | I | N |
| ���룺x | 26 | 9 | 24 | 9 | 14 |
|
| |||||
| ���룺y | 91 | 40 | |||
��ˣ����ԡ��ּ���ת����Ľ���ǡ�9140����
���⣺
��1�������������ԿΪy=3x+13 ʱ�����š��־�����ת����Ľ����
��2��Ϊ���������ı��̶ܳȣ���ҪƵ���ظ�����Կ���������š� �������µ���Կ����ת����õ��±���
| �� �� | �� | �� | ||||
| ƴ �� | Z | I | X | I | N | |
| ���룺x | 26 | 9 | 24 | 9 | 14 | |
|
| ||||||
| ���룺y | 70 | 36 | ||||
���������µ���Կ����ֱ��д�����š������µ���Կ����ת����Ľ����
 ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012ѧ�걱�������������꼶��һѧ����ĩ������ѧ�� ���ͣ������
�Ķ����в��ϣ�
��Ŀ����֪ʵ��a��x����a��2��x��2�����ж� ��
�� �Ĵ�С��ϵ��������˵��.
�Ĵ�С��ϵ��������˵��.
˼·�����á������Ƚ��������Ĵ�С�����г� ��
�� �IJ�
�IJ� ����
����
˵��y�ķ��ż���.[��Դ:Z��xx��k.Com]
�ָ����������ú����������ķ�����
��⣺�ɽ�y�Ĵ���ʽ������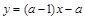 ��Ҫ�ж�y�ķ��ſɽ�������
��Ҫ�ж�y�ķ��ſɽ�������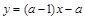 ��ͼ������ʽ��.
��ͼ������ʽ��.
�ο����Ͻ���˼·����������⣺
��֪a��b��c���ǷǸ�����a��5���� ��
�� ��
��
��С��1����1���ֱ��ú�a�Ĵ���ʽ��ʾ4b��4c��
��С��2����2��˵��a��b��c֮��Ĵ�С��ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012�챱�������������꼶��һѧ����ĩ������ѧ�� ���ͣ������
�Ķ����в��ϣ�
��Ŀ����֪ʵ��a��x����a��2��x��2�����ж� ��
��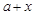 �Ĵ�С��ϵ��������˵��.
�Ĵ�С��ϵ��������˵��.
˼·�����á������Ƚ��������Ĵ�С�����г� ��
��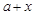 �IJ�
�IJ� ����
����
˵��y�ķ��ż���.[��Դ:Z��xx��k.Com]
�ָ����������ú����������ķ�����
��⣺�ɽ�y�Ĵ���ʽ������ ��Ҫ�ж�y�ķ��ſɽ�������
��Ҫ�ж�y�ķ��ſɽ������� ��ͼ������ʽ��.
��ͼ������ʽ��.
�ο����Ͻ���˼·����������⣺
��֪a��b��c���ǷǸ�����a��5����  ��
�� ��
��
1.��1���ֱ��ú�a�Ĵ���ʽ��ʾ4b��4c��
2.��2��˵��a��b��c֮��Ĵ�С��ϵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com