[题目]在平面直角坐标系中.点(1.2)位于第象限．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】在平面直角坐标系中，点（1，2）位于第　　象限．

【答案】一

【解析】

试题分析：根据平面直角坐标系中各象限点的特征，判断其所在象限，四个象限的符号特征分别是：第一象限（＋，＋）；第二象限（－，＋）；第三象限（－，－）；第四象限（＋，－）。故点（1，2）位于第一象限。

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】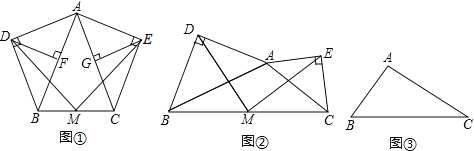

如图①，在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图①所示，其中，DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD，ME，MF，MG．则下列结论正确的是__________（填写序号）

①四边形AFMG是菱形；②△DFM和△EGM都是等腰三角形；③MD=ME；④MD⊥ME．

（2）数学思考：

如图②，在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，M是BC的中点，连接MD和ME，则MD与ME具有怎样的数量和位置关系？请给出证明过程．

（3）类比探究：如图③Rt△ABC中，斜边BC=10，AB=6，分别以AB、AC为斜边作等腰直角三角形ABD和ACE，请直接写出DE的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】下面给出四边形ABCD中的∠A、∠B、∠C、∠D的度数之比，能判定四边形ABCD是平行四边形的是（）.

A. 3:4:4:3B. 4:3:4:3C. 4:3:2:1D. 2:2:3:3

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，AB、CD为两个建筑物，建筑物AB的高度为60m，从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°，测得建筑物CD的底部D点的俯角∠EAD为45°．

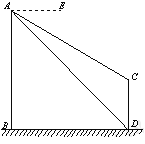
（1）求两建筑物两底部之间的水平距离BD的长度；

（2）求建筑物CD的高度（结果保留根号）．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】分别以下列四组数为一个三角形的边长：①6、8、10；②5、12、13；③8、15、17；④4、5、6．其中能构成直角三角形的有（）

A．1组 B．2组 C．3组 D．4组

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在平面直角坐标系中，点D的坐标是（﹣3，1），点A的坐标是（4，3）．

（1）点B和点C的坐标分别是______、______．

（2）将△ABC平移后使点C与点D重合，点A、B与点E、F重合，画出△DEF．并直接写出E、F的坐标．

（3）若AB上的点M坐标为（x，y），则平移后的对应点M′的坐标为______．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】罗马数字共有 7 个：I（表示 1），V（表示 5），X（表示 10），L（表示 50），C（表示 100），D（表示 500），M（表示 1000），这些数字不论位置怎样变化，所表示的数目都是不变的，其计数方法是用“累积符号”和“前减后加”的原则来计数的：如IX＝10－1＝9，VI＝5＋1＝6，CD＝500－100＝400，则XL＝，XI＝．

查看答案和解析>>

科目：初中数学 来源： 题型：