
【题目】如图,直线![]() (
(![]() )交
)交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
(2)若点![]() 是直线
是直线![]() 上的任意一点,且点
上的任意一点,且点![]() 与点
与点![]() 距离的最小值为4,求该直线表达式;
距离的最小值为4,求该直线表达式;
(3)在(2)的基础上,若点![]() 在第一象限,且
在第一象限,且![]() 为等腰直角三角形,求点
为等腰直角三角形,求点![]() 的坐标.
的坐标.
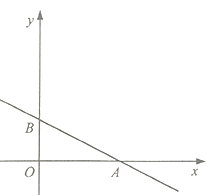
【答案】(1)点![]() 的坐标分别是
的坐标分别是![]() ;(2) y=-
;(2) y=-![]() x+2
x+2![]() ;(3)当点
;(3)当点![]() 的坐标是
的坐标是![]() 或
或![]() 或
或![]() 时,
时,![]() 是等腰直角三角形.
是等腰直角三角形.
【解析】
(1)利用坐标轴上点的特点即可得出结论;
(2)利用直角三角形的面积相等建立方程求出b=2![]() ,即可得出结论;
,即可得出结论;
(3)①当∠ACB=90°时,先判断出四边形ODCE是矩形,得出OD=CE,CD=OE,∠DCE=90°,再判断出△BCE≌△ACD(AAS),得出BE=AD,CE=CD,进而得出AD=4![]() -m,BE=m-2
-m,BE=m-2![]() ,进而用AD=BE建立方程求解即可得出结论;②③当∠BAC=90°和∠ABC=90°时,构造全等三角形即可得出结论.
,进而用AD=BE建立方程求解即可得出结论;②③当∠BAC=90°和∠ABC=90°时,构造全等三角形即可得出结论.
(1)当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,解得
,解得![]() .
.
∴点![]() 的坐标分别是
的坐标分别是![]()
(2)如图,
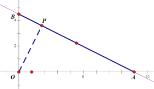
当![]() 时,点
时,点![]() 与点
与点![]() 的距离最小,此时
的距离最小,此时![]() ,
,
∵点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]()
∵![]()
∴![]()
∴![]() ,
,
∴直线AB的解析式为y=-![]() x+2
x+2![]() ;
;
(3)如图,
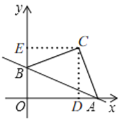
由(1)知,A(4![]() ,0),B(0,2
,0),B(0,2![]() ),
),
∴OA=4![]() ,OB=2
,OB=2![]()
过点C作CD⊥x轴于D,作CE⊥y轴于E,
∵∠DOE=90°,
∴四边形ODCE是矩形,
∴OD=CE,CD=OE,∠DCE=90°,
∴∠BCE+∠BCD=90°,
∵△ABC是等腰直角三角形,
当∠ACB=90°时,
∴BC=AC,∠ACB=90°,
∴∠ACD+∠BCD=90°,
∴∠BCE=∠ACE,
∴△BCE≌△ACD(AAS),
∴BE=AD,CE=CD,
∴设点C坐标为(m,m),
∴AD=OA-OD=4![]() -m,BE=OE-OB=m-2
-m,BE=OE-OB=m-2![]() ,
,
∴4![]() -m=m-2
-m=m-2![]() ,
,
∴m=3![]() ,
,
∴C(3![]() ,3
,3![]() ),
),
如图2,
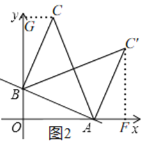
②当∠BAC=90°时,过点C'作C'F⊥x轴于F,
∴∠C'AF+∠AC'F=90°,
∵∠C'AF+∠OAB=90°,
∴∠OAB=∠FC'A,
∵AB=AC',
∴△AOB≌△C'FA(AAS),
∴C'F=OA=4![]() ,AF=OB=2
,AF=OB=2![]() ,
,
∴OF=OA+AF=6![]() ,
,
∴C'(6![]() ,4
,4![]() ),
),
③当∠ABC=90°时,同②的方法得,C(2![]() ,6
,6![]() ),
),
即:点C的坐标为(3![]() ,3
,3![]() )或(6
)或(6![]() ,4
,4![]() )或(2
)或(2![]() ,6
,6![]() ).
).


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:

根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠COE=90° ,OF 平分∠AOE,
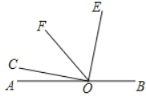
(1)若∠BOE=80°,求∠COF的度数.
(2)若∠COF=α(0°<α<90°),则∠BOE= (用含α的式子表示) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=60cm.
![]()
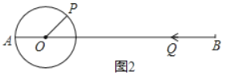
(1)如图1,点P沿线段AB自A点向B点以2厘米/秒运动,同时点Q沿线段BA自B点 向A点以4厘米/秒运动,问经过几秒后P、Q相遇?
(2)在(1)的条件下,几秒钟后,P、Q相距12cm?
(3)如图2,AO=PO=10厘米,∠POB=40°,点P绕着点O以10度/秒的速度顺时针 旋转一周停止,同时点Q沿线段BA自B点向A点运动,假若点P、Q两点能相遇,求点Q运动的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫作△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证: △ABP∽△BCP;
②若PA=3,PC=4,求PB的长;
(2)如图②,已知锐角△ABC,分别以AB,AC为边向外作正△ABE和正△ACD,CE和BD相交于点P,连接AP.
①求∠CPD的度数;
②求证:点P为△ABC的费马点.
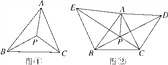
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论:①平面内3条直线两两相交,共有3个交点;②在平面内,若∠AOB =40°,∠AOC= ∠BOC,则∠AOC的度数为20°;③若线段AB=3, BC=2,则线段AC的长为1或5;④若∠a+∠β=180°,且∠a<∠β,则∠a的余角为![]() (∠β-∠a).其中正确结论的个数( )
(∠β-∠a).其中正确结论的个数( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
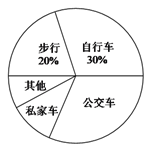
【题目】某校为了解全校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的频数分布直方图和扇形统计图(均不完整).
(1)这次调查中,一共抽取了多少名学生?
(2)补全频数分布直方图;
(3)估计全校所有学生中有多少人乘坐公交车上学.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)分解因式:m2(x﹣y)+4n2(y﹣x);
(2)解不等式组![]() ,并把解集在数轴上表示出来;
,并把解集在数轴上表示出来;
(3)先化简,再求解, ![]() ,其中x=
,其中x=![]() ﹣2.
﹣2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com