
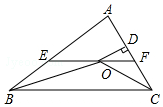
 »ÁÕº£¨‘⁄°˜ABC÷–£¨°œABC∫Õ°œACBµƒ∆Ω∑÷œþœýΩª”⁄µ„O£¨π˝Oµ„◊˜EF°ŒBCΩªAB”⁄µ„E£¨ΩªAC”⁄µ„F£¨π˝µ„O◊˜OD°ÕAC”⁄D£¨œ¬¡–Àƒ∏ˆΩ·¬€£Æ
»ÁÕº£¨‘⁄°˜ABC÷–£¨°œABC∫Õ°œACBµƒ∆Ω∑÷œþœýΩª”⁄µ„O£¨π˝Oµ„◊˜EF°ŒBCΩªAB”⁄µ„E£¨ΩªAC”⁄µ„F£¨π˝µ„O◊˜OD°ÕAC”⁄D£¨œ¬¡–Àƒ∏ˆΩ·¬€£Æ| A£Æ | 1∏ˆ | B£Æ | 2∏ˆ | C£Æ | 3∏ˆ | D£Æ | 4∏ˆ |
∑÷Œˆ ”…‘⁄°˜ABC÷–£¨°œABC∫Õ°œACBµƒ∆Ω∑÷œþœýΩª”⁄µ„O£¨∏˘æðΩ«∆Ω∑÷œþµƒ∂®“”λ˝Ω«–Œƒ⁄Ω«∫Õ∂®¿Ì£¨º¥ø…«Ûµ√¢⁄°œBOC=90°„+$\frac{1}{2}$°œA’˝»∑£ª”…∆Ω––œþµƒ–‘÷ ∫ÕΩ«∆Ω∑÷œþµƒ∂®“µ√≥ˆ°˜BEO∫Õ°˜CFO «µ»—¸»˝Ω«–Œµ√≥ˆEF=BE+CFπ ¢Ÿ’˝»∑£ª”…Ω«∆Ω∑÷œþµƒ–‘÷ µ√≥ˆµ„OµΩ°˜ABC∏˜±þµƒæý¿Îœýµ»£¨π ¢€’˝»∑£ª”…Ω«∆Ω∑÷œþ∂®¿Ì”λ˝Ω«–Œ√ʪ˝µƒ«ÛΩ‚∑Ω∑®£¨º¥ø…«Ûµ√¢€…ËOD=m£¨AE+AF=n£¨‘ÚS°˜AEF=$\frac{1}{2}$mn£¨π ¢Ð’˝»∑£Æ
Ω‚¥ Ω‚£∫°þ‘⁄°˜ABC÷–£¨°œABC∫Õ°œACBµƒ∆Ω∑÷œþœýΩª”⁄µ„O£¨
°ý°œOBC=$\frac{1}{2}$°œABC£¨°œOCB=$\frac{1}{2}$°œACB£¨°œA+°œABC+°œACB=180°„£¨
°ý°œOBC+°œOCB=90°„-$\frac{1}{2}$°œA£¨
°ý°œBOC=180°„-£®°œOBC+°œOCB£©=90°„+$\frac{1}{2}$°œA£ªπ ¢⁄’˝»∑£ª
°þ‘⁄°˜ABC÷–£¨°œABC∫Õ°œACBµƒ∆Ω∑÷œþœýΩª”⁄µ„O£¨
°ý°œOBC=°œOBE£¨°œOCB=°œOCF£¨
°þEF°ŒBC£¨
°ý°œOBC=°œEOB£¨°œOCB=°œFOC£¨
°ý°œEOB=°œOBE£¨°œFOC=°œOCF£¨
°ýBE=OE£¨CF=OF£¨
°ýEF=OE+OF=BE+CF£¨
π ¢Ÿ’˝»∑£ª
π˝µ„O◊˜OM°ÕAB”⁄M£¨◊˜ON°ÕBC”⁄N£¨¡¨Ω”OA£¨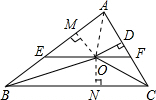
°þ‘⁄°˜ABC÷–£¨°œABC∫Õ°œACBµƒ∆Ω∑÷œþœýΩª”⁄µ„O£¨
°ýON=OD=OM=m£¨
°ýS°˜AEF=S°˜AOE+S°˜AOF=$\frac{1}{2}$AE•OM+$\frac{1}{2}$AF•OD=$\frac{1}{2}$OD•£®AE+AF£©=$\frac{1}{2}$mn£ªπ ¢Ð’˝»∑£ª
°þ‘⁄°˜ABC÷–£¨°œABC∫Õ°œACBµƒ∆Ω∑÷œþœýΩª”⁄µ„O£¨
°ýµ„OµΩ°˜ABC∏˜±þµƒæý¿Îœýµ»£¨π ¢€’˝»∑£Æ
π —°D£Æ
µ„∆¿ ¥ÀÂøº≤È¡ÀΩ«∆Ω∑÷œþµƒ∂®“”Ζ‘÷ £¨µ»—¸»˝Ω«–Œµƒ≈–∂®”Ζ‘÷ £Æ¥Àƒ—∂» ÷–£¨Ω‚µƒπÿº¸ «◊¢“‚ ˝–ŒΩ·∫œÀºœÎµƒ”¶”√£Æ


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | 3$\sqrt{3}$cm | B£Æ | 4$\sqrt{3}$cm | C£Æ | 3$\sqrt{2}$cm | D£Æ | 4$\sqrt{2}$cm |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | x-£®y+z£© | B£Æ | -£®x-y£©+z | C£Æ | x-£®y-z£© | D£Æ | -£®x+y£©+z |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
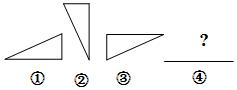 »ÁÕº£¨Ω´“ª∏ˆ÷±Ω«»˝Ω«–Œ∞¥¢Ÿ¢⁄¢€¢ÐµƒÀ≥–Ú“¿¥ŒΩ¯––±‰ªª£¨π€≤ÏÕº–Œµƒ±‰ªªπʬ…£¨»∑∂®¢Ð∂‘”¶µƒÕº–ŒŒ™£®°°°°£©
»ÁÕº£¨Ω´“ª∏ˆ÷±Ω«»˝Ω«–Œ∞¥¢Ÿ¢⁄¢€¢ÐµƒÀ≥–Ú“¿¥ŒΩ¯––±‰ªª£¨π€≤ÏÕº–Œµƒ±‰ªªπʬ…£¨»∑∂®¢Ð∂‘”¶µƒÕº–ŒŒ™£®°°°°£©| A£Æ |  | B£Æ |  | C£Æ | 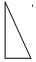 | D£Æ |  |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | 5°Ê | B£Æ | 15°Ê | C£Æ | -5°Ê | D£Æ | 1°Ê |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
 »ÁÕº£¨ƒ≥∫”µÃ”≠ÀÆ∆¬ABµƒ∆¬±»i=1£∫$\sqrt{3}$£¨µÃ∏þBC=5m£¨‘Ú∆¬√ÊABµƒ≥§ «£®°°°°£©
»ÁÕº£¨ƒ≥∫”µÃ”≠ÀÆ∆¬ABµƒ∆¬±»i=1£∫$\sqrt{3}$£¨µÃ∏þBC=5m£¨‘Ú∆¬√ÊABµƒ≥§ «£®°°°°£©| A£Æ | 5 m | B£Æ | 10m | C£Æ | 15 m | D£Æ | 5 m |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | -13°Ê | B£Æ | 13°Ê | C£Æ | -17°Ê | D£Æ | 17°Ê |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | x2=72 | B£Æ | x£®x-1£©=72 | C£Æ | £®x-1£©2=72 | D£Æ | $\frac{x£®x-1£©}{2}$=72 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫—°‘ÒÂ
| A£Æ | x+y=3z | B£Æ | $\frac{1}{x}$-3y=2 | C£Æ | 5x-2y=-1 | D£Æ | xy=3 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com