Question

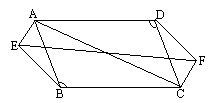
如图，AB∥CD，∠ABC=∠ADC，AE＝CF，BE＝DF．求证：EF与AC互相平分．

Answer 1

答案：
解析：

证明：要证EF和AC互相平分，只须证明AECF是平行四边形．可根据已知条件，首先证出ABCD是平行四边形，得出AD＝BC，AB＝CD．然后再利用三角形全等，证出AE＝CF，AF＝CE，则AECF是平行四边形． 　　连结EC、AF 　　∵AB∥CD，∴∠ABC＋∠BCD＝， 　　∵∠ABC＝∠CDA， 　　∴∠CDA＋∠BCD＝， 　　∴AD∥BC． 　　∴ABCD是平行四边形，∴AB＝CD 　　在△ABE和△CDF中 　　∴△ABE≌△CDF(SSS) 　　∴∠ABE＝∠CDF，∴∠ADF＝∠CBE． 　　在△ADF和△CBE中 　　∴△ADF≌△CBE，∴AF＝EC 　　∴AECF是平行四边形， 　　∴EF与AC互相平分．