
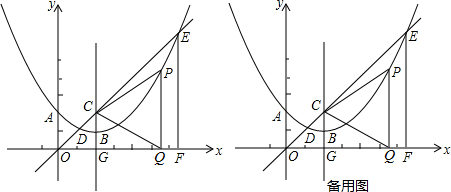
分析 (1)根据抛物线的顶点是(2,1),因而设抛物线的表达式为y=a(x-2)2+1,把A的坐标代入即可求得函数的解析式;
(2)根据△PCQ为等边三角形,则△CGQ中,∠CQD=30°,CG的长度可以求得,利用直角三角形的性质,即可求得CQ,即等边△CQP的边长,则P的纵坐标代入二次函数的解析式,即可求得P的坐标;
(3)解方程组即可求得E的坐标,则EF的长等于E的纵坐标,OE的长度,利用勾股定理可以求得,同理,OC的长度可以求得,则CE的长度即可求解;
(4)可以利用反证法,假设x轴上存在一点,使△CQM≌△CPE,可以证得EM=EF,即M与F重合,与点E为直线y=x上的点,∠CEF=45°即点M与点F不重合相矛盾,故M不存在.
解答 解:(1)设抛物线的表达式为y=a(x-2)2+1,将点A(0,2)代入,得a(0-2)2+1=2,
解这个方程,得a=$\frac{1}{4}$,
∴抛物线的表达式为y=$\frac{1}{4}$(x-2)2+1=$\frac{1}{4}$x2-x+2;
(2)将x=2代入y=x,得y=2
∴点C的坐标为(2,2)即CG=2,
∵△PCQ为等边三角形
∴∠CQP=60°,CQ=PQ,
∵PQ⊥x轴,
∴∠CQG=30°,
∴CQ=4,GQ=2$\sqrt{3}$.
∴OQ=2+2$\sqrt{3}$,PQ=4,
将y=4代入y=$\frac{1}{4}$(x-2)2+1,得4=$\frac{1}{4}$(x-2)2+1
解这个方程,得x1=2+2$\sqrt{3}$=OQ,x2=2-2$\sqrt{3}$<0(不合题意,舍去).
∴点P的坐标为(2+2$\sqrt{3}$,4);
(3)把y=x代入y=$\frac{1}{4}$x2-x+2,得x=$\frac{1}{4}$x2-x+2
解这个方程,得x1=4+2$\sqrt{2}$,x2=4-2$\sqrt{2}$<2(不合题意,舍去)
∴y=4+2$\sqrt{2}$=EF
∴点E的坐标为(4+2$\sqrt{2}$,4+2$\sqrt{2}$)
∴OE=$\sqrt{E{F}^{2}+O{F}^{2}}$=4+4$\sqrt{2}$,
又∵OC=$\sqrt{C{G}^{2}+O{G}^{2}}$=2$\sqrt{2}$,
∴CE=OE-OC=4+2$\sqrt{2}$,
∴CE=EF;
(4)不存在.
如图,假设x轴上存在一点,使△CQM≌△CPE,则CM=CE,∠QCM=∠PCE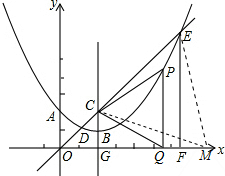
∵∠QCP=60°,
∴∠MCE=60°
又∵CE=EF,
∴EM=EF,
又∵点E为直线y=x上的点,
∴∠CEF=45°,
∴点M与点F不重合.
∵EF⊥x轴,这与“垂线段最短”矛盾,
∴原假设错误,满足条件的点M不存在.
点评 本题考查了待定系数法求二次函数的解析式,以及等边三角形的性质,解直角三角形,反证法,正确求得E的坐标是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
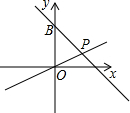 如图,一次函数y=-x+m与y轴交于点B,与正比例函数y=$\frac{1}{2}$x的图象交于点P(2,n).
如图,一次函数y=-x+m与y轴交于点B,与正比例函数y=$\frac{1}{2}$x的图象交于点P(2,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
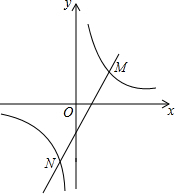 如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$的图象交于点M(2,m)、N(-1,-4)两点,则kx+b>$\frac{a}{x}$的解集为x<-1或x>2.
如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$的图象交于点M(2,m)、N(-1,-4)两点,则kx+b>$\frac{a}{x}$的解集为x<-1或x>2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com