
【题目】已知正方形的每个角等于90°,请解决下列问题:
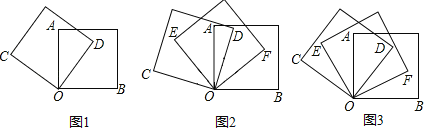
(1)如图1,将两个正方形的一个顶点O重合放置,若∠AOD=50°,求∠COB的度数;
(2)如图2,将三个正方形的一个顶点O重合放置,若∠EOC=40°,∠BOF=30°,求∠AOD的度数;
(3)如图3,将三个正方形的一个顶点O重合放置,若OF平分∠DOB,那么OE平分∠AOC吗?为什么?
【答案】(1)∠COB=130°;(2)∠AOD=20°;(3) OE平分∠AOC,证明见解析.
【解析】
(1)根据正方形各角等于90°,得出∠COD+∠AOB=180°,再根据∠AOD=50°,∠COB=∠COD+∠AOB﹣∠AOD,即可得出答案;
(2)根据已知得出∠1+∠2,∠1+∠3的度数,再根据∠1+∠2+∠3=90°,最后用∠1+∠2+∠1+∠3﹣(∠1+∠2+∠3),即可求出∠1的度数;
(3)根据∠COD=∠AOB和等角的余角相等得出∠COA=∠DOB,∠EOA=∠FOB,再根据角平分线的性质得出∠DOF=∠FOB=![]() ∠DOB和∠EOA=
∠DOB和∠EOA=![]() ∠DOB=
∠DOB=![]() ∠COA,从而得出答案.
∠COA,从而得出答案.
(1)∵两个图形是正方形,
∴∠COD=90°,∠AOB=90°,
∴∠COD+∠AOB=180°,
∵∠AOD=50°,
∴∠COB=∠COD+∠AOB﹣∠AOD=130°;
(2) 如图:∵∠COD=90°,∠AOB=90°,∠EOF=90°,
∴∠COE+∠2+∠1=90°,∠2+∠1+∠3=90°,∠1+∠2+∠BOF=90°,
又∵∠EOC=40°,∠BOF=30°,
∴∠1+∠2=50°①,∠1+∠3=60°②,
又∠1+∠2+∠3=90°③,
①+②﹣③得:∠1=20°;
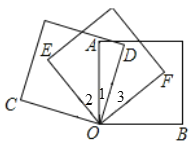
(3)OE平分∠AOC,理由如下:
∵∠COD=∠AOB=90°,
∴∠COD-∠AOD=∠AOB-∠AOD,
即∠COA=∠DOB,
同理:∠EOA=∠FOB,
∵OF平分∠DOB,
∴∠DOF=∠FOB=![]() ∠DOB,
∠DOB,
∴∠EOA=![]() ∠DOB=
∠DOB=![]() ∠COA,
∠COA,
∴OE平分∠AOC.


科目:初中数学 来源: 题型:
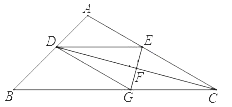
【题目】如图,△ABC中,CD平分∠ACB,CD的垂直平分线分别交AC、DC、BC
于点E、F、G,连接DE、DG.
(1)求证:四边形DGCE是菱形;
(2)若∠ACB=30°,∠B=45°,CG=10,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
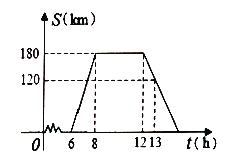
【题目】某地重视生态建设,大力发展旅游业,各地旅游团纷沓而至,某旅游团上午6时从旅游馆出发,乘汽车到距离![]() 的旅游景点观光,该汽车离旅游馆的距离
的旅游景点观光,该汽车离旅游馆的距离![]() 与时间
与时间![]() 的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
(1)求该团旅游景点时的平均速度是多少?
(2)该团在旅游景点观光了多少小时?
(3)求该团返回到宾馆的时刻是几时?
查看答案和解析>>
科目:初中数学 来源: 题型:
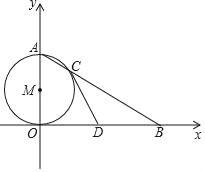
【题目】如图,OA是⊙M的直径,点B在x轴上,连接AB交⊙M于点C.
(1)若点A的坐标为(0,2),∠ABO=30°,求点B的坐标.
(2)若D为OB的中点,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
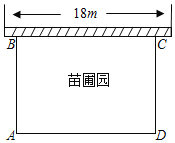
【题目】某中学课外兴趣活动小组准备围建一个矩形的苗圃圆.其中一边靠墙,另外三边用长为40m的篱笆围成.已知墙长为18m(如图所示),设这个苗圃园垂直于墙的一边AB为xm
(1)用含有x的式子表示AD,并写出x的取值范围;
(2)若苗圃园的面积为192m2平方米,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将8个同样大小的小正方体搭成如图所示的几何体,请按照要求解答下列问题:
(1)从正面、左面、上面观察如图所示的几何体,分别画出所看到的几何体的形状图;
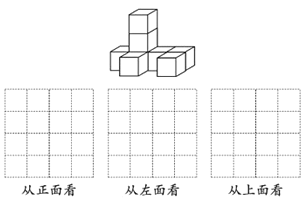
(2)如果在这个几何体上再摆放一个相同的小正方体,并保持这个几何体从上面看和从左面看到的形状图不变.
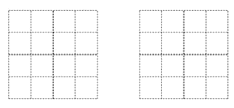
①添加小正方体的方法共有_________种;
②请画出两种添加小正方体后,从正面看到的几何体的形状图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年3月27日是全国中小学生安全教育日,某校为加强学生的安全意识,组织了全校学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整致,满分为10分) 进行统计,绘制了图中两幅不完整的统计图.
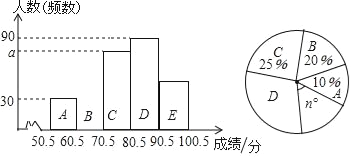
(1)a=_____,n=_____;
(2)补全频数直方图;
(3)该校共有2000名学生.若成绩在70分以下(含70分)的学生安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点(x1,y1),(x2,y2),(x3,y3)都是反比例函数y=﹣![]() 图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
A.x1<x2<x3 B.x1<x3<x2
C.x2<x1<x3 D.x2<x3<x1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=10,AC=16,点M是对角线AC上的一个动点,过点M作PQ⊥AC交AB于点P,交AD于点Q,将△APQ沿PQ折叠,点A落在点E处,当△BCE是等腰三角形时,AP的长为_____.
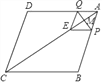
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com