
【题目】已知:如图,在△ABC中,![]() ,以
,以![]() 为直径的⊙O与
为直径的⊙O与![]() 交于点
交于点![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() 的延长线与
的延长线与![]() 的延长线交于点
的延长线交于点![]() .
.
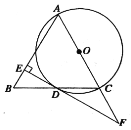
(1)求证:![]() 是⊙O的切线.
是⊙O的切线.
(2)若⊙O的半径为4,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)DE=![]() .
.
【解析】
(1)如图,连接OD,由DE⊥AB可得∠AED=90°,根据等腰三角形的性质可得∠B=∠ACB,∠ODC=∠ACB,根据等量代换可得∠B=∠ODC,可证明OD//AB,可得∠AEF=∠ODF=90°,即可证明DE是⊙O的切线;(2)根据含30°角的直角三角形的性质可求出OF的长,即可求出AF的长,根据含30°角的直角三角形的性质可求出AE的长,利用勾股定理可求出DF、EF的长,进而可求出DE的长.
如图,连接OD
∵DE⊥AB,
∴∠AEF=90°,
∵AB=AC,
∴∠B=∠ACB,
∵OD=OC,
∴∠ODC=∠ACB,
∴∠B=∠ODC,
∴OD//AB,
∴∠ODF=∠AEF=90°,
∵OD是⊙O的半径,
∴DE是⊙O的切线.
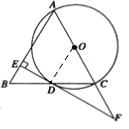
(2)∵∠F=30°,OD=4,OD⊥EF,
∴OF=2OD=8,
∴AF=OF+OA=8+4=12,DF=![]() =
=![]() ,
,
∴AE=![]() AF=6,EF=
AF=6,EF=![]() =
=![]() ,
,
∴DE=EF-DF=![]() -
-![]() =
=![]() .
.


科目:初中数学 来源: 题型:
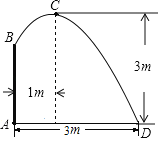
【题目】如图,在喷水池的中心A处竖直安装一个水管AB,水管的顶端安有一个喷水池,使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点![]() ,高度为3m,水柱落地点D离池中心A处3m,以水平方向为
,高度为3m,水柱落地点D离池中心A处3m,以水平方向为![]() 轴,建立平面直角坐标系,若选取
轴,建立平面直角坐标系,若选取![]() 点为坐标原点时的抛物线的表达式为
点为坐标原点时的抛物线的表达式为![]() ,则选取点
,则选取点![]() 为坐标原点时的抛物线表达式为______,水管
为坐标原点时的抛物线表达式为______,水管![]() 的长为______
的长为______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆O的半径为1,六边形ABCDEF是圆O的内接正六边形,从A,B,C,D,E,F六点中任意取两点,并连接成线段.
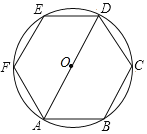
![]() 求线段长为2的概率;
求线段长为2的概率;
![]() 求线段长为
求线段长为![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
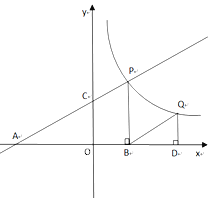
【题目】如图,直线y=![]() x+3分别交 x轴、y轴于点A、C.点P是该直线与双曲线在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=16.
x+3分别交 x轴、y轴于点A、C.点P是该直线与双曲线在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=16.
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点Q与点P在同一个反比例函数的图象上,且点Q在直线PB的右侧,作QD⊥x轴于D,当△BQD与△AOC相似时,求点Q的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的日销售量y(件)与销售价x(元)之间的关系如下表,且日销售量y与销售价x之间满足一次函数关系.
x(元) | 130 | 150 | 165 |
y(件) | 70 | 50 | 35 |
(1)求y与x之间的函数关系式
(2)若该商品的进价是每件120元,商家将每件商品的销售价定为160元时,则每日销售的总利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司一共62辆![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人/辆 | 380元/辆 |
| 20人/辆 | 280元/辆 |
注:载客量指的是每辆客车最多可载该校师生的人数.设学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案总费用最省?最省的总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
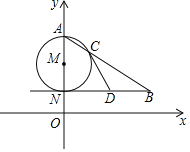
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.
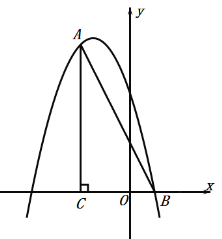
(1)求抛物线的解析式;
(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE最大.
①求点P的坐标和PE的最大值.
②在直线PD上是否存在点M,使点M在以AB为直径的圆上;若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com