
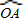 分为三等份,连接MC并延长交y轴于点D(0,3)
分为三等份,连接MC并延长交y轴于点D(0,3)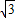 k+b=0.
k+b=0.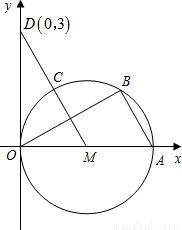
 证明:(1)连接BM,∵B、C把
证明:(1)连接BM,∵B、C把 三等分,∴∠1=∠5=60°,1分
三等分,∴∠1=∠5=60°,1分 ∠5=30°,2分
∠5=30°,2分 OA=OM,∠3=60°,3分
OA=OM,∠3=60°,3分 5分
5分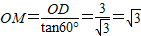 ,
, ,8分
,8分 ,0)代入y=kx+b得:
,0)代入y=kx+b得: k+b=0.
k+b=0.

科目:初中数学 来源:2009年全国中考数学试题汇编《二次函数》(07)(解析版) 题型:解答题
 x+b,经过点M(0,
x+b,经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
查看答案和解析>>
科目:初中数学 来源:2010年浙江省杭州市萧山区中考数学模拟试卷27(沈瑜瑛)(解析版) 题型:解答题
 x+b,经过点M(0,
x+b,经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
查看答案和解析>>
科目:初中数学 来源:2010年浙江省杭州市采荷中学中考数学模拟试卷(5月份)(解析版) 题型:解答题
 x+b,经过点M(0,
x+b,经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
查看答案和解析>>
科目:初中数学 来源:2010年贵州省贵阳市中考适应性考试数学试卷(解析版) 题型:解答题
 x+b,经过点M(0,
x+b,经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).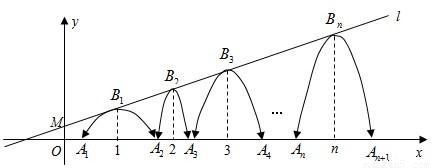
查看答案和解析>>
科目:初中数学 来源:2009年广东省茂名市中考数学试卷(解析版) 题型:解答题
 x+b,经过点M(0,
x+b,经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).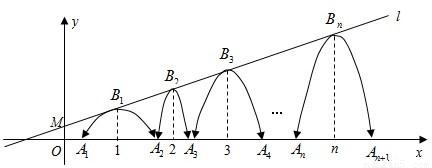
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com