Question

（1）如图1，若⊙O₁与⊙O₂外切于A，BC是⊙O₁与⊙O₂外公切线，B、C为切点，求证：AB⊥AC．
（2）如图2，若⊙O₁与⊙O₂外离，BC是⊙O₁与⊙O₂的外公切线，B、C为切点，连心线O₁O₂分别交⊙O₁、⊙O₂于M、N，BM、CN的延长线交于P，则BP与CP是否垂直？证明你的结论．
（3）如图3，若⊙O₁与⊙O₂相交，BC是⊙O₁与⊙O₂的公切线，B、C为切点，连心线O₁O₂分别交⊙O₁、⊙O₂于M、N，Q是线段MN上一点，连接BQ、CQ，则BQ与CQ是否垂直？证明你的结论．

Answer 1

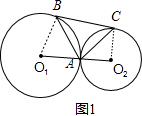
（1）证明：如图1，连接O₁A，O₂C，
∵BC是两圆的外公切线，
∴∠O₁BC=∠O₂CB=90°，
∴O₁B∥O₂C，
∴∠O₁+∠O₂=180°，
∵∠O₁AB=∠O₁BA=（180°-∠O₁）=90°-∠O₁=90°-∠ABC，
∴∠ABC=∠O₁，
同理：∠ACB=∠O₂，
∴∠ABC+∠ACB=（∠O₁+∠O₂）=90°，
∴∠BAC=90°．
∴AB⊥AC；

（2）解：BP⊥CP．
证明：如图2，连接O₁B，O₂C，
∵BC是两圆的外公切线，
∴∠O₁BC=∠O₂CB=90°，
∴O₁B∥O₂C，
∴∠O₁+∠O₂=180°．
∠O₁BM=∠O₁MB=（180°-∠O₁）=90°-∠O₁=90°-∠PBC，
∴∠PBC=∠O₁，
同理：∠PCB=∠O₂，
∴∠PBC+∠PCB=（∠O₁+∠O₂）=90°，
∴∠BPC=90°，
∴BP⊥CP；

（3）解：BQ与CQ不垂直．
证明：如图3，连接O₁B，O₂C，
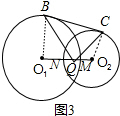
∵BC是两圆的外公切线，
∴∠O₁BC=∠O₂CB=90°，
∴O₁B∥O₂C，
∴∠O₁+∠O₂=180°．
∵O₁B＞O₁Q，
∴∠O₁QB＞∠O₁BQ，
同理：∠O₂QC＞∠O₂CQ，
∴∠O₁QB+∠O₂QC＞∠O₁BQ+∠O₂CQ，
∴∠O₁QB+∠O₂QC＞90°，
∴∠BQC＜90°
∴BQ与CQ不垂直．
分析：（1）连接O₁B，O₂C，根据切线的性质可以得到∠O₁BC=∠O₂CB=90°，再用△O₁AB，△O₂AC的内角和是180°进行证明．
（2）连接O₁B，O₂C，根据切线的性质得到∠O₁BC=∠O₂CB=90°，再用三角形的内角和以及对顶角的性质进行证明．
（3）连接O₁B，O₂C，根据切线的性质得到∠O₁BC=∠O₂CB=90°，然后用三角形中大边对大角以及三角形的内角和定理进行证明．
点评：本题考查圆与圆的位置关系，（1）中两圆是外切的，AB是两圆的公切线，根据切线的性质和三角形内角和定理进行证明．（2）中两圆是外离的，仍然可以用切线的性质和三角形的内角和定理进行证明．（3）中两圆是相交的，先用切线的性质得到90°的角，然后在三角形中用大边对大角以及三角形的内角和证明两直线不垂直．