
分析 在Rt△ABC中,∠C=90°,∠ABC=30°,设AC=x,则BC=$\sqrt{3}$x,AB=2x,延长CB到D点,使AB=DB=2x,则∠D=15°,在Rt△ADC中利用勾股定理计算出AD=($\sqrt{6}$+$\sqrt{2}$)x,然后根据三角函数的定义分别计算15°的正弦、余弦、正切、余切的值.
解答 解:在Rt△ABC中,∠C=90°,∠ABC=30°,
设AC=x,则BC=$\sqrt{3}$x,AB=2x,
延长CB到D点,使AB=DB=2x,则∠D=∠BAD,
∵∠ABC=∠D+∠BAD=30°,
∴∠D=15°,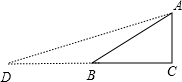
在Rt△ADC中,∵AC=x,CD=2x+$\sqrt{3}$x,
∴AD=$\sqrt{{x}^{2}+(2x+\sqrt{3}x)^{2}}$=($\sqrt{6}$+$\sqrt{2}$)x,
∴sin15°=$\frac{AC}{AD}$=$\frac{x}{(\sqrt{6}+\sqrt{2})x}$=$\frac{\sqrt{6}-\sqrt{2}}{4}$,
cos15°=$\frac{CD}{AD}$=$\frac{(2+\sqrt{3})x}{(\sqrt{6}+\sqrt{2})x}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
tan15°=$\frac{x}{(2+\sqrt{3})x}$=2-$\sqrt{3}$,cot15°=$\frac{CD}{AC}$=$\frac{(2+\sqrt{3})x}{x}$=2+$\sqrt{3}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.


科目:初中数学 来源: 题型:解答题
 配方法不仅可以用来解一元二次方程,还可以用来解决很多问题.
配方法不仅可以用来解一元二次方程,还可以用来解决很多问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
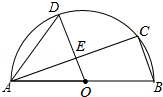 如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm.
如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com