练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．服装市场按每套90元的价格购进40套童装，应缴纳的税费为销售额的10%，如果要获得不低于900元的纯利润，那么每套童装的售价至少是多少元？

    分析 设每套童装的售价是x元，根据售价-进价-税额=利润列出不等式，并解答．

    解答 解：设每套童装的售价是x元，
    依题意得：40x-40×90-40x×10%≥900
    解得x≥125．
    答：每套售价至少为125元．

    点评 本题考查了一元一次不等式的应用．解决问题的关键是读懂题意，找到关键描述语，找到所求的量的数量关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．计算题一：
    （1）-14+|-6|
    （2）（$\frac{2}{3}$-$\frac{1}{4}$）×（-24）
    （3）$\root{3}{-27}$+$\sqrt{16}$-$\sqrt{（-2）^{2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．解方程：
    （1）$\frac{-6+a}{3}$-2a=-$\frac{3}{4}$+$\frac{a}{2}$；
    （2）$\frac{3}{4}$（x-1）-$\frac{2}{5}$（3x+2）=$\frac{1}{10}$-$\frac{3}{2}$（x-1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算
    （1）2x2（3x-2y2）+（-2xy）2
    （2）（2a-b）（2a+3b）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

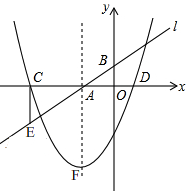    17．如图1，直线l：y=mx+n交x轴，y轴于点A，B，抛物线与x轴交于点C、D，对称轴经过点A，顶点F的纵坐标为-3．CE⊥x轴交直线l于点E（-5，-$\frac{3}{2}$），tan∠BAD=$\frac{1}{2}$．
    （1）求直线l与抛物线的表达式；
    （2）点P是抛物线一动点，当S△CEP=3时，求点P的坐标；
    （3）点M是x轴上一点，点N是在x轴下方抛物线一点，问是否存在这样点M，以点A、B、M、N为顶点的四边形是平行四边形，若存在，请直接写点M的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

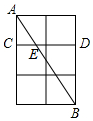    7．如图，在2×3的方格纸中，每个小正方形的边长均为1，点A，B，C，D都在格点上，AB与CD交于点E，则EB的长为$\frac{2\sqrt{13}}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

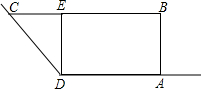    14．某农场拟建一个梯形饲养场ABCD，其中AD，CD分别靠现有墙DM，DN，其余用新墙砌成，墙DM长为9米，墙DN足够长，两面墙形成的角度为135°，新墙DE将饲养场隔成△CDE和矩形ABED两部分．已知新建墙体总长为30米．设AB=x米，梯形饲养场ABCD的面积为S米2．
    （1）求S关于x的函数表达式；
    （2）当x为何值时，饲料场ABCD的面积最大，并求出最大面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

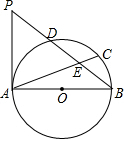    11．如图所示，AB为⊙O的直径，D为$\widehat{AC}$的中点，AC、BD交于点E，P为BD延长线上一点，且PD=DE．
    （1）求证：PA与⊙O相切．
    （2）若AB=10，$\frac{BE}{DE}$=$\frac{7}{9}$，求CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．把（x-y）看成一个整体合并同类项：5（x-y）2+2（x-y）-3（x-y）2+$\frac{1}{2}$（x+y）-3.5．

    查看答案和解析>>

    同步练习册答案