
ЗжЮі ЃЈ1ЃЉЗжСНжжЧщПіЃКЂйЕБBF=$\frac{1}{3}$ABЪБЃЌШчЭМ1ЃЌжЄУїЁїEABЁеЁїFBCЃЌЕУBF=AE=1ЃЌгЩЙДЙЩЖЈРэЧѓГіBEЕФГЄЃЌдйгЩAEЁЮBCЕУ$\frac{AE}{BC}=\frac{EH}{HB}$=$\frac{1}{3}$ЃЌдђBH=$\frac{3}{4}$BEЃЌДњШыЕУГіНсТлЃЛ
ЂкЕБAF=$\frac{1}{3}$ABЪБЃЌШчЭМ2ЃЌЭЌРэЕУ$\frac{AE}{BC}=\frac{EH}{HB}$=$\frac{2}{3}$ЃЌдђBH=$\frac{3}{5}$BEЃЌДњШыЕУГіНсТлЃЛ
злКЯЂйЂкЕУГіHBЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ3ЃЌзїИЈжњЯпЃЌЙЙНЈШЋЕШШ§НЧаЮКЭЕШбќжБНЧШ§НЧаЮЃЌжЄУїЁїAMBЁеЁїBGCЃЌдђBM=CGЃЌAM=BGЃЌгЩЁЯE=45ЁуЃЌЕУЁїAMEЪЧЕШбќжБНЧШ§НЧаЮЃЌдђEG=BMЃЌЫљвдEG=CGЃЛ
ЃЈ3ЃЉзїИЈжњЯпЙЙНЈШЋЕШШ§НЧаЮКЭЕШБпШ§НЧаЮЃЌЯШжЄУїЁїMABЁеЁїFBCКЭЁїMAHЁеЁїKAHЃЌИљОнШЋЕШШ§НЧаЮаджЪКЭШ§НЧаЮФкНЧКЭЖЈРэСаЕШЪНЃЌЧѓГіЁЯP=30ЁуЃЌгЩЕШБпЁїRHBЕУЁЯABH=ЁЯRBCЃЌдђЁїABHЁеЁїCBRЃЌЫљвдRC=AHЃЌдкжБНЧЁїGHCжаРћгУ30ЁуНЧЕФгрЯвСаЪНЕУГіCH=$\frac{CG}{cos30Ёу}$=$\frac{2\sqrt{3}}{3}$CGЃЌМДRH+RC=$\frac{2\sqrt{3}}{3}$CGЃЌДгЖјЕУГіНсТлЃЎ
НтД№ 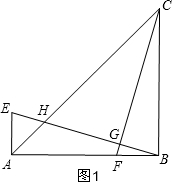 НтЃКЃЈ1ЃЉFЮЊABЕФШ§ЕШЗжЕуЪБЃЌЗжСНжжЧщПіЃК
НтЃКЃЈ1ЃЉFЮЊABЕФШ§ЕШЗжЕуЪБЃЌЗжСНжжЧщПіЃК
ЂйЕБBF=$\frac{1}{3}$ABЪБЃЌШчЭМ1ЃЌ
ЁпЁЯABC=90ЁуЃЌ
ЁрЁЯABE+ЁЯEBC=90ЁуЃЌ
ЁпBHЁЭCFЃЌ
ЁрЁЯBGC=90ЁуЃЌ
ЁрЁЯEBC+ЁЯFCB=90ЁуЃЌ
ЁрЁЯABE=ЁЯFCBЃЌ
ЁпЁЯBAE=ЁЯABC=90ЁуЃЌAB=BCЃЌ
ЁрЁїEABЁеЁїFBCЃЌ
ЁрBF=AE=1ЃЌ
ЁпBF=$\frac{1}{3}$ABЃЌ
ЁрAB=3ЃЌ
гЩЙДЙЩЖЈРэЕУЃКBE=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$ЃЌ
ЁпЁЯEAB+ЁЯABC=90Ёу+90Ёу=180ЁуЃЌ
ЁрAEЁЮBCЃЌ
Ёр$\frac{AE}{BC}=\frac{EH}{HB}$=$\frac{1}{3}$ЃЌ
ЁрBH=$\frac{3}{4}$BE=$\frac{3\sqrt{10}}{4}$ЃЛ
ЂкЕБAF=$\frac{1}{3}$ABЪБЃЌШчЭМ2ЃЌ
ЭЌРэЕУЁїEABЁеЁїFBCЃЌдђAE=BF=1ЃЌ
ЁрAB=$\frac{3}{2}$
гЩЙДЙЩЖЈРэЕУЃКBE=$\sqrt{{1}^{2}+ЃЈ\frac{3}{2}ЃЉ^{2}}$=$\frac{\sqrt{13}}{2}$
ЁпAEЁЮBCЃЌ
Ёр$\frac{AE}{BC}=\frac{EH}{HB}$=$\frac{1}{\frac{3}{2}}$=$\frac{2}{3}$ЃЌ
ЁрBH=$\frac{3}{5}$BE=$\frac{3}{5}$ЁС$\frac{\sqrt{13}}{2}$=$\frac{3\sqrt{13}}{10}$
ЁрHBЕФГЄЮЊ$\frac{3\sqrt{10}}{4}$Лђ$\frac{3\sqrt{13}}{10}$ЃЛ
ЃЈ2ЃЉШчЭМ3ЃЌ Й§AзїAMЁЭBEгкMЃЌдђЁЯAMB=ЁЯBGC=90ЁуЃЌ
Й§AзїAMЁЭBEгкMЃЌдђЁЯAMB=ЁЯBGC=90ЁуЃЌ
ЁпЁЯMAB+ЁЯABM=90ЁуЃЌЁЯABM+ЁЯCBE=90ЁуЃЌ
ЁрЁЯMAB=ЁЯCBEЃЌ
ЁпAB=BCЃЌ
ЁрЁїAMBЁеЁїBGCЃЌ
ЁрBM=CGЃЌAM=BGЃЌ
ЁпЁЯE=45ЁуЃЌAMЁЭBEЃЌ
ЁрЁїAMEЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрAM=EMЃЌ
ЁрEM=BGЃЌ
ЁрEM+MG=BG+MGЃЌ
МДEG=BMЃЌ
ЁрEG=CGЃЛ
ЃЈ3ЃЉ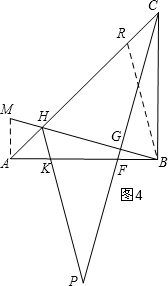 ШчЭМ4ЃЌAH+BH=$\frac{\sqrt{3}}{3}$CPЃЌРэгЩЪЧЃК
ШчЭМ4ЃЌAH+BH=$\frac{\sqrt{3}}{3}$CPЃЌРэгЩЪЧЃК
Й§AзїAMЁЭABЃЌНЛBHбгГЄЯпгкMЃЌ
ЕУЁїMABЁеЁїFBCЃЌ
ЁрAM=BF=AKЃЌЁЯAMB=ЁЯCFBЃЌ
ЁпЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯCAB=45ЁуЃЌ
ЁпЁЯMAB=90ЁуЃЌ
ЁрЁЯMAH=45ЁуЃЌ
ЁрЁЯMAH=ЁЯCABЃЌ
ЁпAH=AHЃЌ
ЁрЁїMAHЁеЁїKAHЃЌ
ЁрЁЯAMB=ЁЯAKHЃЌ
ЁрЁЯAKH=ЁЯCFBЃЌ
ЁпЁЯAKH=ЁЯPKFЃЌЁЯCFB=ЁЯPFKЃЌ
ЁрЁЯPKF=ЁЯPFKЃЌ
ЁпFCЁЭBHЃЌGЪЧPCжаЕуЃЌ
ЁрCH=PHЃЌ
ЁрЁЯAHK=2ЁЯPЃЌ
дкЁїPFKжаЃЌЁЯPKF=$\frac{180Ёу-ЁЯP}{2}$=90Ёу-$\frac{1}{2}$ЁЯPЃЌ
дђ90Ёу-$\frac{1}{2}$ЁЯP+45Ёу+2ЁЯP=180ЁуЃЌ
НтЕУЁЯP=30ЁуЃЌ
дкCHЩЯШЁвЛЕуRЃЌЪЙRH=BHЃЌСЌНгBRЃЌ
ЁрЁЯRHB=$\frac{180Ёу-ЁЯAHK}{2}$=60ЁуЃЌ
ЁрЁїRHBЪЧЕШБпШ§НЧаЮЃЌ
ЁрBH=BR=RHЃЌ
ЁпЁЯCAB=ЁЯACB=45ЁуЃЌЁЯAHB=180Ёу-60Ёу=120ЁуЃЌЁЯBRC=180Ёу-60Ёу=120ЁуЃЌ
ЁрЁЯABH=ЁЯRBCЃЌ
ЁрЁїABHЁеЁїCBRЃЌ
ЁрAH=CRЃЌ
Ёпcos30Ёу=$\frac{CG}{CH}$ЃЌ
ЁрCH=$\frac{CG}{cos30Ёу}$=$\frac{2\sqrt{3}}{3}$CGЃЌ
ЁрRH+RC=$\frac{2\sqrt{3}}{3}$CGЃЌ
ЁпCG=$\frac{1}{2}$PCЃЌRH=BHЃЌBC=AHЃЌ
ЁрAH+BH=$\frac{2\sqrt{3}}{3}$ЁС$\frac{1}{2}$PC=$\frac{\sqrt{3}}{3}$PCЃЎ
ЕуЦР БОЬтЪЧШ§НЧаЮЕФзлКЯЬтЃЌПМВщСЫЕШбќжБНЧШ§НЧаЮЁЂШЋЕШШ§НЧаЮЁЂЕШбќШ§НЧаЮЕШЭМаЮЕФаджЪКЭХаЖЈЃЌзлКЯадНЯЧПЃЛдкЕквЛЮЪжаЃЌFЮЊABЕФШ§ЕШЗжЕуЪБЃЌвЊЗжСНжжЧщПіНјааЬжТлЃЌИљОнЙДЙЩЖЈРэКЭЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэЕУГіНсТлЃЛдкжЄУїСНЬѕЯпЖЮЯрЕШЪБЃЌШчЙћВЛФмжБНгЕУГіЃЌПЩвдПМТЧРћгУЕкШ§ЯпЖЮЕУГіЃЌвВПЩвдРћгУЕШЪНЕФаджЪКЭЯпЖЮЕФКЭВюЙиЯЕЕУГіЃЌБОЬтЕФКѓСНЮЪОЭЪЧРћгУСЫетИіЗНЗЈЃЎ


 ОйвЛЗДШ§ЕЅдЊЭЌВНЙ§ЙиОэЯЕСаД№АИ
ОйвЛЗДШ§ЕЅдЊЭЌВНЙ§ЙиОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
 ШчЭМЃЌдкЕШбќЁїABCжаЃЌЁЯBAC=120ЁуЃЌAB=ACЃЌDЮЊABЕФжаЕуЃЌBEЁЭBCЃЌBE=ADЃЌAEЗжБ№НЛCDгкFЃЌНЛBCгкKЃЎШєDF=1ЃЌдђKCЕФГЄЮЊ$\frac{3\sqrt{21}}{2}$ЃЎ
ШчЭМЃЌдкЕШбќЁїABCжаЃЌЁЯBAC=120ЁуЃЌAB=ACЃЌDЮЊABЕФжаЕуЃЌBEЁЭBCЃЌBE=ADЃЌAEЗжБ№НЛCDгкFЃЌНЛBCгкKЃЎШєDF=1ЃЌдђKCЕФГЄЮЊ$\frac{3\sqrt{21}}{2}$ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
 ШчЭМЃЌЫФБпаЮABCDЪЧОиаЮЃЌЕуEдкЯпЖЮCBЕФбгГЄЯпЩЯЃЌСЌНгDEНЛABгкЕуFЃЌЁЯAED=2ЁЯCEDЃЌЕуGЪЧDFЕФжаЕуЃЌШєBE=1ЃЌDF=7ЃЌдђABЕФГЄЮЊ$\frac{3}{2}\sqrt{5}$ЃЎ
ШчЭМЃЌЫФБпаЮABCDЪЧОиаЮЃЌЕуEдкЯпЖЮCBЕФбгГЄЯпЩЯЃЌСЌНгDEНЛABгкЕуFЃЌЁЯAED=2ЁЯCEDЃЌЕуGЪЧDFЕФжаЕуЃЌШєBE=1ЃЌDF=7ЃЌдђABЕФГЄЮЊ$\frac{3}{2}\sqrt{5}$ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ЃЈx-1 ЃЉ$\sqrt{-x}$ | BЃЎ | ЃЈ1-x ЃЉ$\sqrt{-x}$ | CЃЎ | -ЃЈx+1 ЃЉ$\sqrt{x}$ | DЃЎ | ЃЈx-1 ЃЉ $\sqrt{x}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
 ШчЭМЃЌАбвЛИіГЄЗНаЮжНЬѕABCDбиEFелЕўЃЌШєЁЯEFG=55ЁуЃЌдђЁЯAEG=70ЁуЃЎ
ШчЭМЃЌАбвЛИіГЄЗНаЮжНЬѕABCDбиEFелЕўЃЌШєЁЯEFG=55ЁуЃЌдђЁЯAEG=70ЁуЃЎВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com