
����Ŀ��ij��λΪ����Ӧ������������ȫ�������ĺ��٣������ڳ��Ϳ��ֱ�Ϊ20m��16m�ľ��δ�������һ��40m2�ľ��ν�����ABCD���ý�����������ǽ�������������ô����ľ�ǽ��(��ͼΪƽ��ʾ��ͼ)����ÿ���ǽ���������õľ�ǽ�ڳ��Ȳ��ó����䳤�ȵ�һ�룬��֪װ��ǽ�ڵķ���Ϊ20Ԫ/m2���½�(��װ��)ǽ�ڵķ���Ϊ80Ԫ/m2���轡������3m��������AB�ij�Ϊxm��BC�ij�Ϊym����������ǽ�ڵ���Ͷ��ΪwԪ��
��1����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����w��x�ĺ�����ϵʽ�������������������AB��Ϊ8mʱ��Ͷ��Ϊ����Ԫ��

���𰸡���1��y��![]() ��5��x��10������2��w=300����x+
��5��x��10������2��w=300����x+![]() ������x=8ʱ��w��3900��Ԫ����
������x=8ʱ��w��3900��Ԫ����
��������
��1������ʽ��Լ��Ա���ȡֵ��Χֻ����ݡ������õľ�ǽ�ڳ��Ȳ��ó����䳤�ȵ�һ�롱���������
��2����Ͷ���������ֹ��ɣ���ǽ���½�ǽ��Ӧ�ø��ݣ�1���н���������������ú�x��ʽ�ӷֱ��ʾ������������⣮
�⣺��1�����������֪y��![]() ��
��
��
��5��x��10
��2���������֪w=��x+![]() ����3��80+��x+
����3��80+��x+![]() ����3��20=300����x+
����3��20=300����x+![]() ����
����
��x=8ʱ��w��300(8+![]() )��3900��Ԫ����
)��3900��Ԫ����


 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
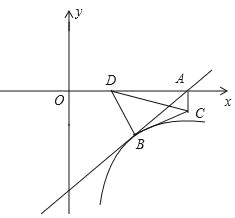
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=kx��10������A��12��0����B��a����5����˫����y=![]() ������B��
������B��
��1����ֱ��y=kx��10��˫����y=![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2����C�ӵ�A�������ع���A��y��ƽ�е�ֱ�������˶����ٶ�Ϊÿ��1����λ���ȣ���C���˶�ʱ��Ϊt��0��t��12��������BC����BD��BC��x���ڵ�D������CD��
������C��˫������ʱ����t��ֵ��
����0��t��6��Χ�ڣ���BCD�Ĵ�С��������仯����tan��BCD�ı仯��Χ������������仯����tan��BCD��ֵ��
����DC=![]() ʱ����ֱ��д��t��ֵ��
ʱ����ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
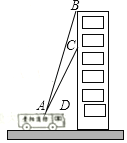
����Ŀ��������ij����֧����һ������¥ǰ����������ϰ����ͼ��ʾ�������ٱ��������ݳɹ��ȳ���C��������ߺ�����C�����Ϸ�17��B������һ������ߣ������ٱ������������ݽ���ȳ�����֪��A�����¥��ˮƽ������15�ף�����A���õ�һ��ʩ��ʱ������ˮƽ�ߵļнǡ�CAD=60�㣬��ڶ���ʩ��ʱ������ˮƽ�ߵļнǡ�BAD�Ķ����������ȷ��1�㣩��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л��Ļ���ԴԶ�����������μǡ����������塷��ˮ䰴�������¥�Ρ����ҹ��Ŵ���ƪС˵�еĵ��ʹ���������Ϊ���Ĵ�ŵ���������ijУҪ��û�ж����Ĵ�������ѧ������ѡ�����������μǡ������������塷����ˮ䰴�������¥�Ρ����μ�ΪA��B��C��D��ÿ��������ѡ���Ļ�����ȣ�
��1��ѧ��С��ƻ�ѡ��������������ǡ��ѡ�������μǡ��͡�ˮ䰴��������������ĸ���Ϊ���٣�
��2����ѧ��С����С�ո��ƻ�ѡ��һ����������������ǡ��ѡ��ͬһ�������ĸ���Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ƻ������ס������ֲ�Ʒ��2500�֣�ÿ����1�ּײ�Ʒ�ɻ������0.3��Ԫ��ÿ����1���Ҳ�Ʒ�ɻ������0.4��Ԫ����ù��������˼ײ�Ʒx���֣��������ס������ֲ�Ʒ��õ�������Ϊy����Ԫ����
��1����y��x֮��ĺ�������ʽ��
��2����ÿ����1�ּײ�Ʒ��ҪAԭ��0.25�֣�ÿ����1���Ҳ�Ʒ��ҪAԭ��0.5�֣����г�Ӱ�죬�ó��ܻ�õ�Aԭ������Ϊ1000�֣�����ԭ�ϳ��㣮����ù��������ס������ֲ�Ʒ��Ϊ���ٶ�ʱ���ܻ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������龳��
��ͼ1���ı���ABCD�������Σ�M��BC���ϵ�һ�㣬E��CD�ߵ��е㣬AEƽ����DAM��

��̽��չʾ��
��1��֤����AM=AD+MC��
��2��AM=DE+BM�Ƿ�������������������֤����������������˵�����ɣ�
����չ���졿
��3�����ı���ABCD�dz��������ȵľ��Σ������������䣬��ͼ2��̽��չʾ��1������2���еĽ����Ƿ��������ֱ������жϣ�����Ҫ֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
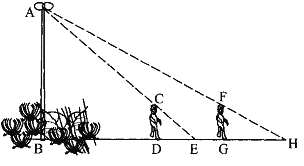
����Ŀ����ͼ����������һ·�Ƹ�AB. �ڵƹ��£�С����D�㴦��Ӱ��DE=3�ף���BD�������ߵ���G�㣬DG=5�ף���ʱС����Ӱ��GH��5��. ���С��������Ϊ1.7�ף���·�Ƹ�AB�ĸ߶�(��ȷ��0.1��)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
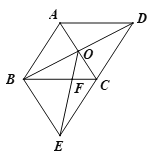
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O,��ABC=60�㣬����B��AC��ƽ���߽�DC���ӳ����ڵ�E.
(1) ��֤���ı���ABECΪ���Σ�
(2) ��AB=6������OE����OE��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90����BC�Ĵ�ֱƽ����DE��BC��D����AB��E��F��DE�ϣ���AF=CE=AE��
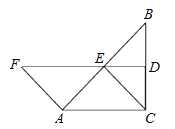
��1��˵���ı���ACEF��ƽ���ı��Σ�
��2������B����ʲô����ʱ���ı���ACEF�����Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com