
 如图,已知凸五边形ABCDE的边长均相等,且∠DBE=∠ABE+∠CBD,AC=1,则BD必定满足( )
如图,已知凸五边形ABCDE的边长均相等,且∠DBE=∠ABE+∠CBD,AC=1,则BD必定满足( )| A. | BD<2 | B. | BD=2 | ||
| C. | BD>2 | D. | 以上情况均有可能 |
分析 据∠DBE=∠ABE+∠CBD,且△BED的内角和为180°,得出得出∠AED+∠CDE=180°,判定AE∥CD,由AE=CD,推出四边形AEDC为平行四边形推出DE=AC.则BC=CD=DE=1,推出BD<BC+CD=2.
解答 证明:∵AE=AB,
∴∠ABE=∠AEB,同理∠CBD=∠CDB
∵∠ABC=2∠DBE,
∴∠ABE+∠CBD=∠DBE,
∵∠ABE=∠AEB,∠CBD=∠CDB,
∴∠AEB+∠CDB=∠DBE,
∴∠AED+∠CDE=180°,
∴AE∥CD,
∵AE=CD,
∴四边形AEDC为平行四边形.
∴DE=AC=AB=BC.
∴△ABC是等边三角形,
∴BC=CD=1,
在△BCD中,∵BD<BC+CD,
∴BD<2.
故选A.
点评 本题主要考查等腰三角形的性质:等腰三角形的底角相等,以及等边三角形的判定定理.解题时注意,同旁内角互补,两直线平行.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:填空题
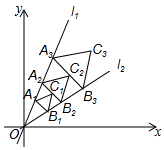 如图,点A1(1,$\sqrt{3}}$)在直线l1:y=$\sqrt{3}$x上,过点A1作A1B1⊥l1交直线l2:y=$\frac{{\sqrt{3}}}{3}$x于点B1,以A1B1为边在△OA1B1外侧作等边三角形A1B1C1,再过点C1作A2B2⊥l1,分别交直线l1和l2于A2,B2两点,以A2B2为边在△OA2B2外侧作等边三角形A2B2C2,…按此规律进行下去,则第n个等边三角形AnBnCn的面积为$\frac{\sqrt{3}}{2}$$(\frac{3}{2})^{2n-3}$.(用含n的代数式表示)
如图,点A1(1,$\sqrt{3}}$)在直线l1:y=$\sqrt{3}$x上,过点A1作A1B1⊥l1交直线l2:y=$\frac{{\sqrt{3}}}{3}$x于点B1,以A1B1为边在△OA1B1外侧作等边三角形A1B1C1,再过点C1作A2B2⊥l1,分别交直线l1和l2于A2,B2两点,以A2B2为边在△OA2B2外侧作等边三角形A2B2C2,…按此规律进行下去,则第n个等边三角形AnBnCn的面积为$\frac{\sqrt{3}}{2}$$(\frac{3}{2})^{2n-3}$.(用含n的代数式表示)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -$\sqrt{2}$ | C. | -1 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在直角坐标平面内,△ABC的顶点A(-1,0),点B与点A关于原点对称,AB=BC,∠CAB=30°,将△ABC绕点C旋转,使点A落在x轴上的点D处,点B落在点E处,那么BE所在直线的解析式为y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$.
如图,在直角坐标平面内,△ABC的顶点A(-1,0),点B与点A关于原点对称,AB=BC,∠CAB=30°,将△ABC绕点C旋转,使点A落在x轴上的点D处,点B落在点E处,那么BE所在直线的解析式为y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 白纸张数 | 1 | 2 | 3 | 4 | 5 | … |
| 纸条长度 | 40 | 75 | 110 | 145 | 180 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com