练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．有理数a、b在数轴上的对应的位置如图所示，则下列各式①a+b＜0；②a-b＞0；③ab＞0；④|a|＞b；⑤1-b＞0；⑥a+1＜0，一定成立的有（　　）
    A．3个B．4个C．5个D．6个

    分析 根据数轴确定a，b的范围，即可解答．

    解答 解：由数轴可得：a＜-1＜0＜b＜1，
    a+b＜0；a-b＜0；ab＜0；|a|＞b；1-b＞0；a+1＜0，
    正确的有：①④⑤⑥，共4个；
    故选：B．

    点评 本题考查了数轴，解决本题的关键确定a，b的范围．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．如图，一块正方形，边长是18cm，上面横竖各有两道黑条（阴影部分），宽度都是2cm，请利用平移的知识求出图中白色部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，△ABO的顶点A、B、O均在格上，请你画出△ABO绕点O旋转180°后的△A1B1O．（不要求写作法、证明，但要在所画的三角形中标上顶点字母）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

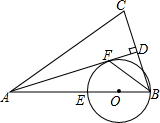    4．如图，在△ABC中，AB=AC，AD是BC边上的高线，BF平分∠ABC交AD于点F，以AB上的点O为圆心，OB为半径的⊙O交AB于点E，恰好经过点F．
    （1）求证：AD与⊙O相切；
    （2）当BC=4，AC=6时，求线段AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．两块等腰直角三角板ABC，DEF按图1的方式放置在同一条直线l上，点C与点F重合，线段EB绕点E逆时针旋转45°交AD于点M．已知∠ABC=∠DEF=90°，DE=2．
    （1）求证：AM=DM；
    （2）将图1中的三角板ABC沿直线l向左平移，如图2所示，设CE=x．
    ①求$\frac{AM}{DM}$的值（用含x的代数式表示）；
    ②若将图2中的三角板ABC绕点C逆时针旋转m°（0＜m＜45），原题中的其它条件保持不变，如图3所示，请探究：$\frac{AM}{DM}$的值是否发生变化，若有变化，请求出$\frac{AM}{DM}$的值（用含x的代数式表示）；若没有变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．如图，OD平分∠AOB，过点D作CD∥OB交OA于C，若∠D=36°，则∠ACD=（　　）
    A．54°B．60°C．63°D．72°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图1，在△ABC中，点D是BC的中点，延长AD到点G，使DG=AD，连接CG，可以得到△ABD≌△GCD，这种作辅助线的方法我们通常叫做“倍长中线法”．
    如图2，在△ABC中，点D是BC的中点，点E是AB上一点，连接ED，小明由图1中作辅助线的方法想到：延长ED到点G，使DG=ED，连接CG．
    （1）请直接写出线段BE和CG的关系：BE=CG；
    （2）如图3，若∠A=90°，过点D作DF⊥DE交AC于点F，连接EF，已知BE=3，CF=2$\sqrt{5}$，其它条件不变，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（1，$\sqrt{3}$），将线段OA绕原点O逆时针旋转30°，得到线段OB，则点B的坐标是（　　）
    A．（0，2）B．（2，0）C．（1，-$\sqrt{3}$）D．（-1，$\sqrt{3}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．在直角坐标系中，△ABO的顶点坐标分别为O（0，0）、A（2a，0）、B（0，-a），线段EF两端点坐标为（-m，a+1），F（-m，1），（2a＞m＞a）；直线l∥y轴交x轴于P（a，0），且线段EF与CD关于y轴对称，线段CD与NM关于直线l对称．
    （1）求点N、M的坐标（用含m、a的代数式表示）；
    （2）△ABO与△MFE通过平移能重合吗？能与不能都要说明其理由，若能请你说出一个平移方案（平移的单位数用m、a表示）

    查看答案和解析>>

    同步练习册答案