
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ�����������ᡱ��ͼ�е�A��ʾ��10����B��ʾ10����C��ʾ18�����dzƵ�A�͵�C�����������28�����ȵ�λ������P�ӵ�A��������2��λ/����ٶ����š��������ᡱ���������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룻��P�ӵ�A������ͬʱ����Q�ӵ�C��������1��λ/����ٶ����š��������ᡱ�ĸ������˶�������P����B��ʱ����P��Q��ֹͣ�˶������˶���ʱ��Ϊt�룮�ʣ�
��1���ú�t�Ĵ���ʽ��ʾ����P���˶������о�O��ľ��룻
��2��P��Q��������ʱ���������ʱ�估������M����Ӧ�����Ƕ��٣�
��3���Ƿ����P��O���������������ij�����Q��B���������������ij������ʱ�������ڣ���ֱ��д��t��ȡֵ���������ڣ���˵�����ɣ�

���𰸡���1��![]() ����2������ʱ��Ϊ
����2������ʱ��Ϊ![]() �룬��M����Ӧ������
�룬��M����Ӧ������![]() ����3�����ڣ�t��2��t��
����3�����ڣ�t��2��t��![]() ��
��
��������
��1���ֵ�P��AO�Ϻ͵�P��OB������������������P��ÿ��ʱt��ȡֵ��Χ���ٸ�������ֱ��г�����ʽ�ɵô𰸣�
��2����������ʱP��Q�˶���ʱ����ȣ�P��Q�˶��ľ���͵���28�ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
��3����0��t��5��5��t��8��8��t��15�������������PO=BQ���ɵ÷��̣��ֱ������̣��ɵô𰸣�
�⣺��1���趯��P���˶������о�O��ľ���ΪS����P��A�˶���Oʱ,����ʱ��Ϊ��![]() ���룩��
���룩��
��0��t��5ʱ��S��10��2t��
��P��O�˶���Bʱ,����ʱ��Ϊ��![]() ���룩
���룩
��P��A�˶���Bʱ,����ʱ��Ϊ��15��
��5��t��15ʱ��S��t��5��
������P���˶������о�O��ľ���S��![]() ��
��
��2���辭��a�룬P��Q�������������P�˶��ľ���Ϊ10+��a-5������Q�˶��ľ���Ϊa,
10+��a-5��+a=28
��ã�a��![]() ��
��
���M����Ӧ�����ǣ�18��![]() ��
��![]() ��
��
����M����Ӧ������![]() ��
��
��3�����ڣ�t��2��t��![]() ��
��
���ɣ���0��t��5ʱ��
10��2t����18��10��t����1��
��ã�t��2
��5��t��8ʱ��
��t��10��2����1����18��10��t����1��
��ã�t��![]() ��
��
��8��t��15ʱ��
��t��10��2����1��[t����18��10����1]��1
�÷����⣬
�ʴ��ڣ�t��2��t��![]() ��
��
�ʴ�Ϊ����1��![]() ����2������ʱ��Ϊ
����2������ʱ��Ϊ![]() �룬��M����Ӧ������
�룬��M����Ӧ������![]() ����3�����ڣ�t��2��t��
����3�����ڣ�t��2��t��![]() ��
��


 �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д� ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����ͬѧ�ļ���ѧУ�ľ����Ϊ3000�ף���ͬѧ�Ȳ���600�ף�Ȼ��˹�����ȥѧУ����ͬѧ�����г�ȥѧУ����֪�ײ����ٶ����������г��ٶȵ�![]() �����������ٶ����������г��ٶȵ�2����������ͬѧͬʱ�Ӽҷ�ȥѧУ�������ͬѧ����ͬѧ�絽2���ӣ�
�����������ٶ����������г��ٶȵ�2����������ͬѧͬʱ�Ӽҷ�ȥѧУ�������ͬѧ����ͬѧ�絽2���ӣ�
��1�����������г����ٶȣ�
��2��������ѧУʱ����ͬѧ��ѧУ���ж�Զ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ɴ�1��ʼ��������Ȼ����ɣ����8�е�8 ������________����n �е�һ�����ɱ�ʾΪ___��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
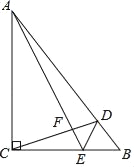
����Ŀ����ͼ����ABC����ACB=90������D��E�ֱ���AB��BC�ϣ�AC=AD����CDE=45�㣬CD��AE���ڵ�F������AEC=��DEB��CE=![]() ����CF=______��
����CF=______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�����Ϊ1�����ᣬ����ͬѧ�������ۣ����ۺ������ϵ�һ�е�����1���ڶ��е�����13�������е�����43���������˹��ɣ������е������� ��

A. 183 B. 157 C. 133 D. 91
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�������㣺�۲�����ʽ��
1��3=1��4+3=7 3�ѣ���1��=3��4��1=11 5��4=5��4+4=24 4�ѣ���3��=4��4��3=13
��1��������һ�룺a��b= ��
��2����a��b����ôa��b b��a��������=�������١� ��
��3����a�ѣ���2b��=3������� ��a��b���ѣ�2a+b����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
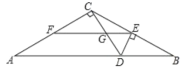
����Ŀ����ͼ����֪EF�ǡ�ABC����λ�ߣ�DE��BC��AB�ڵ�D��CD��EF���ڵ�G,��CD��AC,EF=8��EG=3����AC�ij�Ϊ___________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˹�������籭��ȼ��ͬѧ�Ƕ������˶������飬ijѧУ������ס�������Ʒ�Ƶ�����ѧ��ʹ�ã���֪��1000 Ԫ��������������������1600Ԫ�������������������ͬ����������ĵ��۱���������ĵ�����30Ԫ��
��1����ס�������Ʒ�Ƶ�����ĵ��۸��Ƕ���Ԫ��
��2��ѧ֦��һ���Թ���ס�������Ʒ�Ƶ�����25�������ܷ��ò�����1610Ԫ����ô����ѧУ������ٸ�����Ʒ�Ƶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
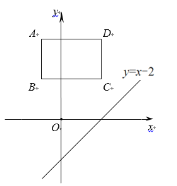
����Ŀ����ͼ���ı���ABCD�Ǿ��Σ�AD��![]() �ᣬ��B������Ϊ (-1��2)����D������Ϊ(2��4)����ֱ��y=x-2����ƽ��m����λ��ʹƽ�ƺ��ֱ��ǡ�þ�����D .
�ᣬ��B������Ϊ (-1��2)����D������Ϊ(2��4)����ֱ��y=x-2����ƽ��m����λ��ʹƽ�ƺ��ֱ��ǡ�þ�����D .
��1����m��ֵ��
��2��ƽ�ƺ��ֱ������εı�BC���ڵ�E�����CDE�����.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com