
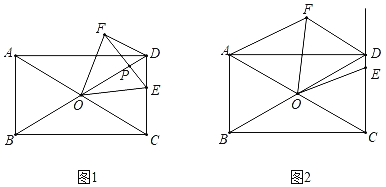
【题目】如图1,在矩形ABCD中,AB=1,对角线AC,BD相交于点O,∠COD=60°,点E是线段CD上一点,连接OE,将线段OE绕点O逆时针旋转60°得到线段OF,连接DF.
(1)求证:DF=CE;
(2)连接EF交OD于点P,求DP的最大值;
(3)如图2,点E在射线CD上运动,连接AF,在点E的运动过程中,若AF=AB,求OF的长.
【答案】(1)详见解析;(2)![]() ;(3)OF=1或
;(3)OF=1或![]() .
.
【解析】
(1)证明△FOD≌△EOC(SAS),则可得出结论;
(2)证明△FDP∽△ODE,可得出![]() ,设DF=CE=x,则DE=1﹣x,则
,设DF=CE=x,则DE=1﹣x,则![]() ,得出DP=﹣x2+x=
,得出DP=﹣x2+x=![]() ,由二次函数的性质可得出答案;
,由二次函数的性质可得出答案;
(3)分情况讨论:①如图1,过点F作FM⊥AD于点M,证明△AOF是等边三角形,得出OF=1;②过点A作AN⊥DF于点N,则∠FDA=30°,证明△OAF≌△AOD(SAS),得出OF=AD=![]() .
.
(1)证明:由题意知∠FOE=∠DOC=60°,
∴∠FOE﹣∠DOE=∠DOC﹣∠DOE,即∠FOD=∠EOC,
在矩形ABCD中,AC=BD=2OC=2OD,
∴OC=OD,
又∵OF=OE,
∴△FOD≌△EOC(SAS),
∴DF=CE;
(2)解:在△ODC中,OD=OC,∠COD=60°,
∴△OCD是等边三角形,∠OCD=60°,
又△FOD≌△EOC,
∴∠FDO=∠ECO=60°,
在△OEF中,OE=OF,∠EOF=60°,
∴△OEF是等边三角形,∠OEF=60°,
∴180°﹣∠FDP﹣∠FPD=180°﹣∠OEP﹣∠OPE,即∠DFP=∠DOE,
又∠FDP=∠ODE=60°,
∴△FDP∽△ODE,
∴![]() ,
,
设DF=CE=x,则DE=1﹣x,
∴![]() ,
,
∴DP=﹣x2+x=![]() ,
,
∴DP的最大值为![]() ;
;
(3)解:①在矩形ABCD中,AB=1,∠COD=60°,
∴AD=![]() ,∠OAD=∠ODA=30°,
,∠OAD=∠ODA=30°,
∴∠FDA=∠FDO﹣∠ODA=30°,
如图1,过点F作FM⊥AD于点M,
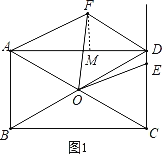
设FM=m,则MD=![]() m,AM=
m,AM=![]() -
-![]() m,
m,
又∵AF=AB=1,
∴在Rt△AFM中,AM2+FM2=AF2,
∴![]() ,
,
∴m1=![]() ,m2=1(舍去),
,m2=1(舍去),
∴sin∠FAM=![]() ,
,
∴∠FAM=30°,
∴∠FAO=60°,且AF=AB=AO,
∴△AOF是等边三角形,
∴OF=1;
②如图2,过点A作AN⊥DF于点N,则∠FDA=30°,
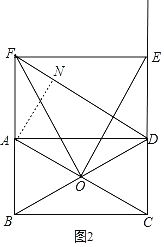
∴∠DAN=60°,AN=![]() ,
,
∴cos∠FAN=![]() ,
,
∴∠FAN=30°,
∴∠FAO=120°,
又∠AOD=120°,
∴∠FAO=∠AOD,
又AF=AO=OD,
∴△OAF≌△AOD(SAS),
∴OF=AD=![]() .
.
综合以上可得,OF=1或![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
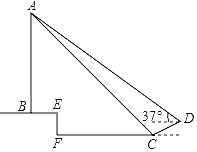
【题目】一天,小战和同学们一起到操场测量学校旗杆高度,他们首先在斜坡底部C地测得旗杆顶部A的仰角为45°,然后上到斜坡顶部D点处再测得旗杆顶部A点仰角为37°(身高忽略不计).已知斜坡CD坡度i=1:2.4,坡长为2.6米,旗杆AB所在旗台高度EF为1.4米,旗台底部、台阶底部、操场在同一水平面上.则请问旗杆自身高度AB为( )米.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
A.10.2B.9.8C.11.2D.10.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线Cn:yn=![]() x2+(n-1)x+2n (其中n为正整数)与x轴交于An,Bn.两点(点An在Bn的左边)与y轴交于点Dn.
x2+(n-1)x+2n (其中n为正整数)与x轴交于An,Bn.两点(点An在Bn的左边)与y轴交于点Dn.
(1)填空:①当n=1时,点A1的坐标为______,点B1的坐标为______;
②当n=2时,点A2的坐标为______,点B2的坐标为______;
(2)猜想抛物线Cn是否经过某一个定点,若经过请写出该定点坐标并给予证明:若不经过,请说明理由;
(3)猜想![]() 的大小,并给予证明.
的大小,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
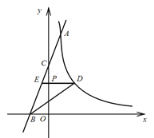
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图像交于点
的图像交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值和反比例函数的表达式;
的值和反比例函数的表达式;
(2)在![]() 轴上有一动点
轴上有一动点![]()
![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交反比例函数的图像于点
轴的直线,交反比例函数的图像于点![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
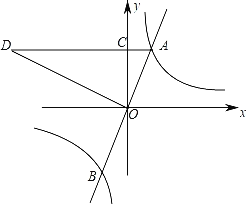
【题目】如图,直线y1=2x与双曲线y2=![]() 交于点A,点B,过点A作AC⊥y轴于点C,OC=2,延长AC至D,使CD=4AC,连接OD.
交于点A,点B,过点A作AC⊥y轴于点C,OC=2,延长AC至D,使CD=4AC,连接OD.
(1)求k的值;
(2)求∠AOD的大小;
(3)直接写出当y1>y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某口罩加工厂有![]() 两组工人共
两组工人共![]() 人,
人,![]() 组工人每人每小时可加工口罩
组工人每人每小时可加工口罩![]() 只,
只,![]() 组工人每人每小时可加工口罩
组工人每人每小时可加工口罩![]() 只,
只,![]() 两组工人每小时一共可加工口罩
两组工人每小时一共可加工口罩![]() 只.
只.
(1)求![]() 两组工人各多少人;
两组工人各多少人;
(2)由于疫情加重![]() 两组工人均提高了工作效率,一名
两组工人均提高了工作效率,一名![]() 组工人和一名
组工人和一名![]() 组工人每小时共可生产口罩
组工人每小时共可生产口罩![]() 只,若
只,若![]() 两组工人每小时至少加工
两组工人每小时至少加工![]() 只口罩,那么
只口罩,那么![]() 组工人每人每小时至少加工多少只口罩?
组工人每人每小时至少加工多少只口罩?
查看答案和解析>>
科目:初中数学 来源: 题型:
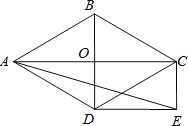
【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C. D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2![]() 时,求EA的长。
时,求EA的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
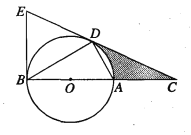
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为1,∠CBD=30°,则图中阴影部分的面积;
(3)过点B作⊙O的切线交CD的延长线于点E若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有3个分别写有数字﹣2,0,1的小球,它们除了数字不同以外其余完全相同,先从盒子里随机抽取1个小球,再从剩下的小球中抽取1个,将这两个小球上的数字依次记为a,b,则满足关于x的方程x2+ax+b=0有实数根的概率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com