
如下图,在Rt△ABC中,已知AB=BC=CA=4 cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1 cm/s;点P沿CA、AB向终点B运动,速度为2 cm/s,设它们运动的时间为x(s).
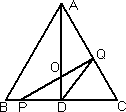
(1)求x为何值时,PQ⊥AC;
(2)设△PQD的面积为y(cm2),当0<x<2时,求y与x的函数关系式;
(3)当0<x<2时,求证:AD平分△PQD的面积;
(4)探索以PQ为直径的圆与AC的位置关系.请写出相应位置关系的x的取值范围(不要求写出过程)
|
(1)∵当Q在AB上时,显然PQ不垂直于AC. 当,由题意得:BP=x,CQ=2x,PC=4-x, ∴AB=BC=CA=4,∠C=60°, 若PQ⊥AC,则有∠QPC=30°,∴PC=2CQ ∴4-x=2×2x,∴x= ∴当x= (2)当0<x<2时,P在BD上,Q在AC上,过点Q作QH⊥BC于H, ∵∠C=60°,QC=2x,∴QH=QC×sin60°=x ∵AB=AC,AD⊥BC,∴BD=CD= ∴DP=2-x,∴y= (3)当0<x<2时,在Rt△QHC中,QC=2x,∠C=60°, ∴HC=x,∴BP=HC ∵BD=CD,∴DP=DH, ∵AD⊥BC,QH⊥BC,∴AD∥QH, ∴OP=OQ ∴S△PDO=S△DQO, ∴AD平分△PQD的面积; (4)显然,不存在x的值,使得以PQ为直径的圆与AC相离 当x= 当0≤x< |


科目:初中数学 来源: 题型:
| 3 | 8 |
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(湖北黄石卷)数学(解析版) 题型:选择题
如下图,在Rt△ABC中,∠ACB=900,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为
A.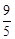 B.
B.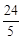 C.
C.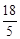 D.
D.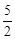
查看答案和解析>>
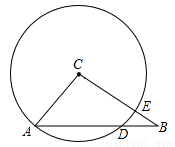
科目:初中数学 来源:2012-2013学年江苏省盐城市中考模拟数学试卷(解析版) 题型:解答题
如下图,在Rt△ABC中,∠ACB=90°,D是AB边上任意的一点(异于A、B),以BD为直径的⊙0与边AC相切于点E,连结DE并延长,与BC的延长线交于点F.
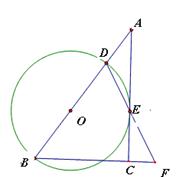
(1)求证:BD=BF;
(2)若BC=12,AD=8,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com