
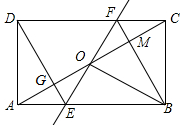
 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S四边形DGOF=2:7.其中正确结论的个数是( )
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S四边形DGOF=2:7.其中正确结论的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 ①利用线段垂直平分线的性质的逆定理可得结论;
②在△EOB和△CMB中,对应直角边不相等,则两三角形不全等;
③可证明∠CDE=∠DFE;
④设S△EGO=x,则S△AOE=2x,S△BOF=4x,可通过面积转化进行解答.
解答 解:①∵矩形ABCD中,O为AC中点,
∴OB=OC,
∵∠COB=60°,
∴△OBC是等边三角形,
∴OB=BC,
∵FO=FC,
∴FB垂直平分OC,
故①正确;
②∵△BOC为等边三角形,
∴OB=BC,
∵FO=FC,BF=BF,
∴△BCF≌△BOF,
∴∠BOF=∠BCF=90°,
∴BO⊥EF,
∵BF⊥OC,
∴∠CMB=∠EOB=90°,
∴BO≠BM,
∴△EOB与△CMB不全等;
故②错误;
③易知△ADE≌△CBF,∠1=∠2=∠3=30°,
∴∠ADE=∠1=30°,∠BEO=60°
∴∠CDE=60°,∠DFE=∠BEO=60°,
∴∠CDE=∠DFE,
∴DE=EF,
故③正确;
④易知△AOE≌△COF,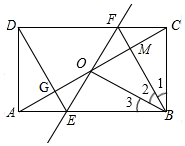
∴S△AOE=S△COF,
∵S△COF=2S△CMF,
∵∠FCO=30°,
∴FM=$\frac{CM}{\sqrt{3}}$,BM=$\sqrt{3}$CM,
∴$\frac{FM}{BM}$=$\frac{1}{3}$,
∴S△FOM:S△BOF=1:4,
易证△GEO≌△MFO,
∴S△GEO=S△MFO,
易证明四边形DEBF是平行四边形,
∴S△DEF=S△EFB=2S△BOF,
设S△EGO=x,则S△AOE=2x,S△BOF=4x,
S四边形DGOF=S△DEF-S△EGO=S△EFB-S△EGO=8x-x,
∴S△AOE:S四边形DGOF=2x:(8x-x)=2:7,
故④正确;
所以其中正确结论的个数为3个;
故选B.
点评 本题综合性比较强,既考查了矩形的性质、等腰三角形的性质,又考查了全等三角形的性质和判定,及线段垂直平分线的性质,内容虽多,但不复杂;看似一个选择题,其实相当于四个证明题,属于常考题型.


科目:初中数学 来源: 题型:选择题
| 年龄(单位:岁) | 13 | 14 | 15 | 16 |
| 频数(单位:名) | 5 | 15 | x | 10-x |
| A. | 平均数、中位数 | B. | 平均数、方差 | C. | 众数、中位数 | D. | 众数、方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4cm,6cm,11cm | B. | 4cm,5cm,lcm | C. | 3cm,4 cm,5 cm | D. | 2cm,3 cm,6 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点E是正方形ABCD内一点,连接BE、CE、DE,AB=CE.
如图,点E是正方形ABCD内一点,连接BE、CE、DE,AB=CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
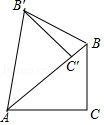 如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在斜边AB上,连接BB′,则∠C′B′B的度数为( )
如图,把Rt△ABC绕点A逆时针旋转40°,得到Rt△AB′C′,点C′恰好落在斜边AB上,连接BB′,则∠C′B′B的度数为( )| A. | 40° | B. | 50° | C. | 70° | D. | 20° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品名 | 单价(台/元) |
| 电视机 | 5000 |
| 洗衣机 | 2000 |
| 空调 | 2400 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
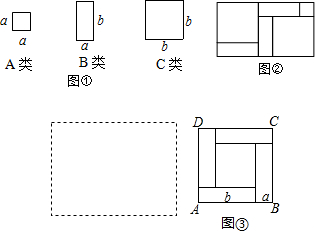 如图,有足够多的边长为a的小正方形(A类),长为b宽为a的长方形(B类)以及边长为b的大正方形(C类)
如图,有足够多的边长为a的小正方形(A类),长为b宽为a的长方形(B类)以及边长为b的大正方形(C类)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com