
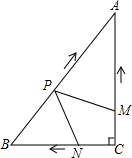
 时,以A、P、M为顶点的三角形与△ABC相似
时,以A、P、M为顶点的三角形与△ABC相似 时,四边形APNC的面积S有最小值,其最小值是
时,四边形APNC的面积S有最小值,其最小值是
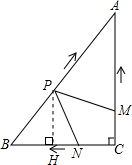
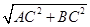 =5cm.
=5cm. ,即
,即 ,
, ;
;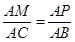 ,即
,即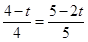 ,
, 时,以A、P、M为顶点的三角形与△ABC相似;
时,以A、P、M为顶点的三角形与△ABC相似; ,即
,即 ,
, t,
t, ×3×4-
×3×4- ×(3-t)•
×(3-t)• t,
t,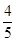 (t-
(t- )2+
)2+ (0<t<2.5).
(0<t<2.5).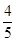 >0,
>0, 时,S最小值=
时,S最小值= .
. 时,四边形APNC的面积S有最小值,其最小值是
时,四边形APNC的面积S有最小值,其最小值是 .
.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
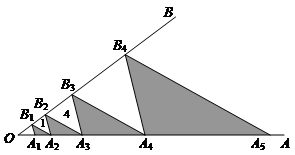
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.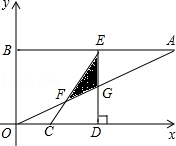
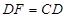 ?
?查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 B.
B.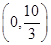
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
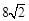 ,则△CEF的周长是 .
,则△CEF的周长是 .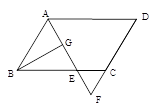
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com