Question

已知AB在平面直角坐标系中的位置如图所示，每个小正方形的边长为单位1．
（1）在x轴上找一点C，画出△ABC，使△ABC是以AB为底的等腰三角形，并写出点C的坐标：______．
（2）将△ABC绕着点C分别按顺时针方向旋转90°、180°、270°，画出旋转后的图形，并说出A点的对应点坐标分别为______，______，______．
（3）试欣赏你画出的图形，想一想：整个图形______轴对称图形（填“是”或“不是”）；若是，有______条对称轴．整个图形______中心对称图形（填“是”或“不是”）；若是，对称中心是______点．

Answer 1

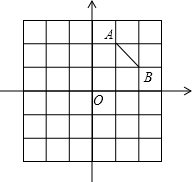
解：（1）所画图形如下：
C点坐标为：（0，0）；

（2）所画图形如上．
根据坐标图及各点的位置即可得出：A′（2，-1），A′′（-1，-2），A′′′（-2，1）．
（3）根据所花图形可得：是对称图，有4条对称轴；也是中心对称图形，C是中心对称点．
故答案为：（0，0），（2，-1），（-1，-2），（-2，1）；是，4，是C．
分析：（1）可将C点放在原点，这样构成以AB为底的等腰三角形．
（2）根据旋转角度、旋转方向、旋转中心找到各点的对称点，顺次连接即可．
（3）根据（2）所画的图形结合轴对称、中心对称的性质及特点即可作出回答．
点评：本题考查旋转作图及等腰三角形的性质，难度不大，但综合了很多知识，注意细心解答．