
【题目】好街坊橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共 30 台,用去了 5520 元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过 8850 元的资金采购电饭煲和电压锅共 50 台,且电饭煲的利润不少于电压锅的利润的![]() ,问橱具店有哪几种进货方案?并说明理由;
,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
【答案】(1) 橱具店在该买卖中赚了1380元;(2)有三种方案:①购买电饭煲19台,购买电压锅31台;②购买电饭煲20台,购买电压锅30台;③购买电饭煲21台,购买电压锅29台;(3) 购进电饭煲21台、电压锅各29台时,橱具店赚钱最多
【解析】
(1)设橱具店购进电饭煲x台,电压锅y台,根据橱具店购进这两种电器共30台且用去了5520元,即可得出关于x、y的二元一次方程组,解之即可得出x、y的值,再根据总利润=单个利润×购进数量即可得出结论;
(2)设购买电饭煲![]() 台,则购买电压锅
台,则购买电压锅![]() 台,根据已知列不等式组,即可得出关于
台,根据已知列不等式组,即可得出关于![]() 的一元一次不等式组,解之即可得出a的取值范围,由此即可得出各进货方案;
的一元一次不等式组,解之即可得出a的取值范围,由此即可得出各进货方案;
(3)根据总利润=单个利润×购进数量分别求出各进货方案的利润,比较后即可得出结论.
(1)设橱具店购进电饭煲x台,电压锅y台,
根据题意得:![]() ,
,
解得:![]() ,
,
∴18×(250-200)+12×(200-160)=1380(元).
答:橱具店在该买卖中赚了1380元;
(2)设购买电饭煲![]() 台,则购买电压锅(
台,则购买电压锅(![]() )台,
)台,
根据题意得: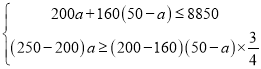 ,
,
解得:![]() ,
,
又∵![]() 为正整数,
为正整数,
∴![]() 可取19,20,21.
可取19,20,21.
故有三种方案:
①购买电饭煲19台,购买电压锅31台;
②购买电饭煲20台,购买电压锅30台;
③购买电饭煲21台,购买电压锅29台;
(3)设橱具店赚钱数额为w元,![]() ,
,
∵10>0,
∴![]() 随
随![]() 的增大而增大,
的增大而增大,
∴当![]() 时,
时,![]() 有最大值,
有最大值,
即购进电饭煲21台、电压锅各29台时,橱具店赚钱最多.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B分别在x轴、y轴的正半轴上,OA=4,AB=5,点D在反比例函数![]() (k>0)的图象上,
(k>0)的图象上,![]() ,点P在y轴负半轴上,OP=7.
,点P在y轴负半轴上,OP=7.
(1)求点B的坐标和线段PB的长;
(2)当![]() 时,求反比例函数的解析式。
时,求反比例函数的解析式。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区某校组织了一次“诗词大会”,张老师为了选拔本班学生参加,对本班全体学生诗词的掌握情况进行了调查,并将调查结果分为了三类:A:好,B:中,C:差.请根据图中信息,解答下列问题:
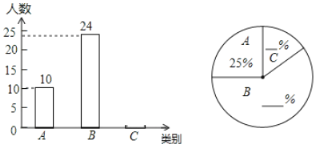
(1)全班学生共有 人;
(2)扇形统计图中,B类占的百分比为 %,C类占的百分比为 %;
(3)将上面的条形统计图补充完整;
(4)小明被选中参加了比赛.比赛中有一道必答题是:从下表所示的九宫格中选取七个字组成一句诗,其答案为“便引诗情到碧霄”.小明回答该问题时,对第四个字是选“情”还是选“青”,第七个字是选“霄”还是选“宵”,都难以抉择,若分别随机选择,请用列表或画树状图的方法求小明回答正确的概率.
情 | 到 | 碧 |
霄 | 诗 | 青 |
引 | 宵 | 便 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AO为Rt△ABC的角平分线,∠ACB=90°,以O为圆心,OC为半径的圆分别交AO,BC于点D,E,连接ED并延长交AC于点F.

(1)求证:AB是⊙O的切线;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于点A和点B(3,0),与
轴交于点A和点B(3,0),与![]() 轴交于点C(0,3),P是线段BC上一点,过点P作PN∥
轴交于点C(0,3),P是线段BC上一点,过点P作PN∥![]() 轴交
轴交![]() 轴于点N,交抛物线于点M.
轴于点N,交抛物线于点M.
(1)求该抛物线的表达式;
(2)如果点P的横坐标为2,点Q是第一象限抛物线上的一点,且△QMC和△PMC的面积相等,求点Q的坐标;
(3)如果![]() ,求tan∠CMN的值.
,求tan∠CMN的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在任意四边形ABCD中,AC,BD是对角线,E、F、G、H分别是线段BD、BC、AC、AD上的点,对于四边形EFGH的形状,某班的学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
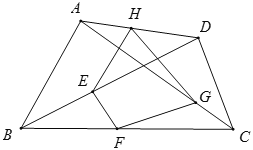
A. 当E,F,G,H是各条线段的中点时,四边形EFGH为平行四边形
B. 当E,F,G,H是各条线段的中点,且AC⊥BD时,四边形EFGH为矩形
C. 当E,F,G,H是各条线段的中点,且AB=CD时,四边形EFGH为菱形
D. 当E,F,G,H不是各条线段的中点时,四边形EFGH可以为平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AC=4,AB=2,将矩形ABCD绕点A旋转得到矩形AB'C'D',使点B的对应点B'落在AC上,B'C'交AD于点E,在B'C'上取点F,使B'F=AB.
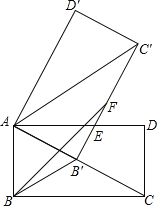
(1)求证:AE=C'E;
(2)求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
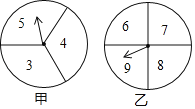
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 的函数表达式为
的函数表达式为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线
为半径画圆,交直线![]() 于点
于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线
为半径画圆,交直线![]() 于点
于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线
为半径画圆,交直线![]() 于点
于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ;…按此做法进行下去,其中
;…按此做法进行下去,其中![]() 的长为_______.
的长为_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com