
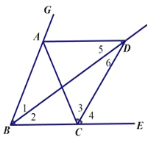
【题目】如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:AB=AD;
(2)求证:CD平分∠ACE.
(3)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.

【答案】(1)证明见解析;(2)证明见解析;(3)∠BDC=![]() ∠BAC,证明见解析
∠BAC,证明见解析
【解析】
(1)根据平行线的性质得到∠ADB=∠DBC,由角平分线的定义得到∠ABD=∠DBC,等量代换得到∠ABD=∠ADB,根据等腰三角形的判定即可得到AB=AD;(2)根据平行线的性质得到∠ADC=∠DCE,由①知AB=AD,等量代换得到AC=AD,根据等腰三角形的性质得到∠ACD=∠ADC,求得∠ACD=∠DCE,即可得到结论;
(3)根据角平分线的定义得到∠DBC=![]() ∠ABC,∠DCE=
∠ABC,∠DCE=![]() ∠ACE,由于∠BDC+∠DBC=∠DCE于是得到∠BDC+
∠ACE,由于∠BDC+∠DBC=∠DCE于是得到∠BDC+![]() ∠ABC=∠ACE,由∠BAC+∠ABC=∠ACE,于是得到∠BDC+
∠ABC=∠ACE,由∠BAC+∠ABC=∠ACE,于是得到∠BDC+![]() ∠ABC=
∠ABC=![]() ∠ABC+
∠ABC+![]() ∠BAC,即可得到结论.
∠BAC,即可得到结论.
证明:
![]() (1) AD∥BE
(1) AD∥BE
![]() ∠2= ∠5
∠2= ∠5
![]() AD平分∠GBE
AD平分∠GBE
![]() ∠2= ∠1
∠2= ∠1
![]() ∠1= ∠5 , AB= AD
∠1= ∠5 , AB= AD
(2) ![]() AB= AD AB= ACAC= AD
AB= AD AB= ACAC= AD
![]() ∠3= ∠ADC
∠3= ∠ADC
![]() 又AD∥BE ∠ADC= ∠4
又AD∥BE ∠ADC= ∠4
![]() ∠3= ∠4
∠3= ∠4
![]() CD平分∠ACE
CD平分∠ACE
(3)∠BDC=![]() ∠BAC
∠BAC
![]()
![]() 证明:BD平分∠ABE
证明:BD平分∠ABE
∴∠2= ∠1 = ![]() ∠ABC
∠ABC
根据三角形外角性质得:
∠1+ ∠2+ ∠BAC=∠4 +∠3①
①式两边除以2得![]() ∠BAC=∠4-∠2
∠BAC=∠4-∠2
而由∠2+ ∠6 =∠4 得出∠6 =∠4 -∠2 即∠BDC=∠4 -∠2
∠BDC=![]() ∠BAC
∠BAC


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=6cm,∠B=∠C,BC=4cm,点D为AB的中点.
(1)如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以1.5cm/s的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过_____秒后,点P与点Q第一次在△ABC的AC边上相遇?(在横线上直接写出答案,不必书写解题过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正方形ABCD的边长为5,点E在边AB上,AE=3,延长DA至点F,使AF=AE,连结EF.将△AEF绕点A顺时针旋转![]() (0°<
(0°<![]() <90°),如图2所示,连结DE、BF.
<90°),如图2所示,连结DE、BF.
(1)请直接写出DE的取值范围:_______________________;
(2)试探究DE与BF的数量关系和位置关系,并说明理由;
(3)当DE=4时,求四边形EBCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列关于![]() 的分式方程:
的分式方程:
方程1. ![]() , 方程2.
, 方程2. ![]() , 方程3.
, 方程3. ![]() , ……,方程n,
, ……,方程n,
【1】填空:分式方程1的解为 ,分式方程2的解为 ;
【2】解分式方程3;
【3】根据上述方程的规律及解的特点,直接写出方程n及它的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】火车站有某公司待运的甲种货物1530吨,乙种货物1150吨,现计划用50节A,B两种型号的车厢将这批货物运至北京,已知每节A型车厢的运费是0.5万元,每节B型车厢的运费是0.8万元;甲种货物35吨和乙种货物15吨可装满一节A型车厢,甲种货物25吨和乙种货物35吨可装满一节B型车厢,按此要求安排A,B两种车厢的节数,共有哪几种方案?请你设计出所有方案,并说明哪种方案的运费最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x | ··· | 1 | 2 | 3 | 5 | 7 | 9 | ··· |
y | ··· | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | ··· |
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为________;
②该函数的一条性质:__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
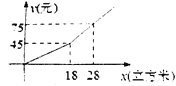
【题目】为了增强人们的节约用水意识,环节城市用水压力。某市规定,每月用水18立方米以内(含18立方米)和用水18立方米以上采取两种不同的收费标准.下图为该市的用户每月应交水费y(元)关于用水量x(立方米)的函数图像.思考并回答下列问题:
(1)求出用水量小于18立方米时,每月应交水费y(元)关于用水量x(立方米)的函数表达式.
(2)若小明家某月交水费81元,则这个月用水量为多少立方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com