【题目】如图，已知△ABC是等边三角形，D为边AC的中点，AE⊥EC，BD=EC．
（1）求证：△BDA≌△CEA；
（2）请判断△ADE是什么三角形，并说明理由．
【答案】（1）证明见解析；（2）△ADE是等边三角形，证明见解析．
【解析】
试题分析：本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△BDA≌△CEA是解题的关键．（1）易证∠ACE=∠CBD，BC=AC，即可证明△BDA≌△CEA，即可解题；
（2）根据（1）中结论可得AE=CD，根据直角三角形中30°角所对直角边是斜边一半的性质可得DE=AD，即可解题．
试题解析：
（1）∵D是AC中点，
∴∠CBD=∠ABD=30°，∠BDA=90°，
∵∠ACB=60°，
∴∠ACE=30°，
在△BDA和△CEA中，
，
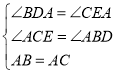∴△BDA≌△CEA（AAS）；
（2）∵△BDA≌△CEA，
∴AE=CD，
∵RT△AEC中，∠ACE=30°，
∴DE=
AC=AD，
∵AD=CD，
∴AD=DE=AE．
∴△ADE是等边三角形．
一线名师提优试卷系列答案科目：初中数学 来源： 题型：
【题目】先阅读下面的例题，再解答后面的题目．
例：已知x2+y2﹣2x+4y+5＝0，求x+y的值．
解：由已知得（x2﹣2x+1）+（y2+4y+4）＝0，
即（x﹣1）2+（y+2）2＝0．
因为（x﹣1）2≥0，（y+2）2≥0，它们的和为0，
所以必有（x﹣1）2＝0，（y+2）2＝0，
所以x＝1，y＝﹣2．
所以x+y＝﹣1．
题目：已知x2+4y2﹣6x+4y+10＝0，求xy的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
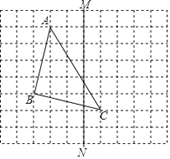
【题目】如图，在长度为1个单位的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
(1)在图中画出与△ABC关于直线MN成轴对称的△A1B1C1；(不写画法)
(2)请你判断△ABC的形状，并求出AC边上的高．
查看答案和解析>>
科目：初中数学 来源： 题型：
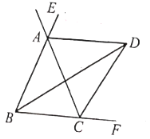
【题目】如图，
，
，
，
分别平分
的外角
，内角
，外角
．以下结论：①
；②
；③
；④平分
；⑤
．其中正确的结论有______________．（把正确结论序号填写在横线上）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直角三角形纸片的两直角边长分别为6、8，按如图那样折叠，使点A与点B重合，折痕为DE，则S△BCE：S△BDE等于（ ）
A．2：5 B．14：25 C．16：25 D．4：21
查看答案和解析>>
科目：初中数学 来源： 题型：
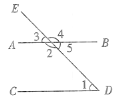
【题目】如图,直线AB，CD被DE所截，则∠1和 是同位角，∠1和 是内错角，∠1和 是同旁内角；
(2)在(1)中，如果∠5=∠1,那么∠1=∠3的推理过程如下,请在括号内注明理由：
因为∠5=∠1( )，
∠5=∠3( )，
所以∠1=∠3( ).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1)填表：
a | 0.000 001 | 0.001 | 1 | 1 000 | 1 000 000 |
|
(2)由上表你发现了什么规律?请用语言叙述这个规律：______________________________.
(3)根据你发现的规律填空：
①已知
=1.442,则
=__________,
=__________；
②已知
=0.076 96,则
=__________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将一个等腰直角三角形按图示方式依次翻折，则下列说法正确的个数有（ ）
①DF平分∠BDE；②△BFD是等腰三角形；；③△CED的周长等于BC的长.
A. 0个； B. 1个； C. 2个； D. 3个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
