
���� ��1�����̳���һ�ι���Ŀյ�ÿ̨������xԪ��������Ŀ�������̳�����52000Ԫ�ļ۸��ٴι�������ͺŵĿյ��������ǵ�һ�ι����2����������ĵ����ϵ���200Ԫ��ÿ̨���ۼ�Ҳ�ϵ���200Ԫ���г���ʽ���̽�ɣ�
��2������ཫy̨�յ����۳��ۣ�������Ŀ�������������οյ������л�õ������ʲ�����22%�����㽫�ڶ��ι���IJ��ֿյ���ÿ̨�����۳��ۡ��г�����ʽ����ɣ�
��� �⣺
��1�����̳���һ�ι���Ŀյ�ÿ̨������xԪ���������з��̵ã�
$\frac{24000}{x}��2$=$\frac{52000}{x+200}$��
��ã�x=2400��
������x=2400��ԭ���̵ĸ���
���̳���һ�ι���Ŀյ�ÿ̨������2400Ԫ��
��2���轫y̨�յ����۳��ۣ��������⣬�ã�
3000��$\frac{24000}{2400}$+��3000+200����0.95y+��3000+200������$\frac{52000}{2400+200}$-y���ݣ�24000+52000������1+22%����
��ã�y��8��
����ཫ8̨�յ����۳��ۣ�
���� ���⿼���˷�ʽ���̵�Ӧ�ú�һԪһ�β���ʽ��Ӧ�ã����÷�ʽ���̽�Ӧ����ʱ��һ����Ŀ�л���������ȹ�ϵ����ʱҪ������Ŀ��Ҫ��������⣬ѡ�����е�һ����ȹ�ϵ��Ϊ�з��̵����ݣ�����һ����������δ֪��������ʽ����ʱ����Ҫһ��Ҫע�������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
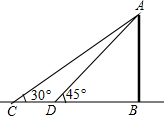 ��ͼ���Ӷ���ˮ��AB����C���������A������Ϊ30�㣬����ǰ��12m����D����D�����A������Ϊ45�㣬�����ߣ�
��ͼ���Ӷ���ˮ��AB����C���������A������Ϊ30�㣬����ǰ��12m����D����D�����A������Ϊ45�㣬�����ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
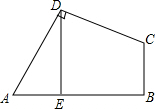 ��ͼ�����ı���ABCD�У���ADC=��ABC=90�㣬AD=DC��DE��AB��E�����ı���ABCD�����Ϊ12����DE�ij���
��ͼ�����ı���ABCD�У���ADC=��ABC=90�㣬AD=DC��DE��AB��E�����ı���ABCD�����Ϊ12����DE�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
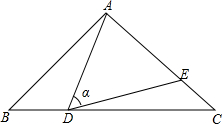 ��ͼ���ڡ�ABC�У�AB=AC=10��BC=16����D�DZ�BC�ϣ�����B��C�غϣ�һ���㣬��ADE=��B=����DE��AC�ڵ�E�����н��ۣ�
��ͼ���ڡ�ABC�У�AB=AC=10��BC=16����D�DZ�BC�ϣ�����B��C�غϣ�һ���㣬��ADE=��B=����DE��AC�ڵ�E�����н��ۣ�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��3��8�� | B�� | ��3��-8�� | C�� | ��8��3�� | D�� | ��-8��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x-3y+1 | B�� | 3x+y=z | C�� | x2-5y=1 | D�� | x+2y=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
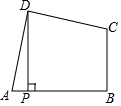 ��ͼ�����ı���ABCD�У���ADC=��ABC=90�㣬AD=CD��DP��AB��P�����ı���ABCD�������18����DP�ij��ǣ�������
��ͼ�����ı���ABCD�У���ADC=��ABC=90�㣬AD=CD��DP��AB��P�����ı���ABCD�������18����DP�ij��ǣ�������| A�� | 3$\sqrt{3}$ | B�� | 2$\sqrt{3}$ | C�� | 3$\sqrt{2}$ | D�� | $\frac{9}{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com